The Vindication of Magnitude-Based Inference Will G
Hopkins, Alan M Batterham Sportscience 22, 19-29, 2018
(sportsci.org/2018/mbivind.htm) |
||||||
|
Authors' note. This article was published as a draft with post-publication peer
review. We invited readers to make supportive or critical comments using this template and submit as an attachment in an email to us. We published comments via this page
following any minor editing and interaction. This version incorporates points
raised in comments to date (24 August 2018). Future comments may be included
in a further update. The draft version with tracked changes resulting in this
version is available as a docx here. The
changes from the draft version are as follows… ·
From
the comments of Little (2018) and Lakens (2018), and our response (Batterham and Hopkins, 2018), MBI can be described as reference Bayesian inference with a
dispersed uniform prior. Two paragraphs starting here have been augmented. ·
The
comment of Wilkinson
(2018) supports our interpretation of errors
and error rates in MBI. We see no need
to modify our article in this respect. ·
When
the editor of Medicine and Science in
Sports and Exercise announced rejection of manuscripts using MBI, we
published a
comment (Hopkins and Batterham, 2018) recommending use of the Bayesian
description of MBI. We noted that the probability thresholds used by the
Intergovernmental Panel on Climate Change are remarkably similar to those of
MBI, and we have updated this article accordingly here. We also critiqued an attack on MBI
by a journalist who used Sainani's erroneous error rates in a news item. We
noted two potentially damaging effects of the news item and of Sainani's
critique and include them here as an extra paragraph, followed by a paragraph
on avoiding underpowered studies. ·
The
comment of Buchheit
(2018) highlights the plight of a researcher
who understands and has opted for MBI, and for whom (in the absence of viable
alternatives) a return to p values is unthinkable. His comment represents an
endorsement of MBI by an experienced practitioner-researcher who suffered
under p values. No update of this article is required. ·
Some
researchers still need to understand how MBI works and how p values fail to
adequately represent uncertainty in effects. One of us (WGH) therefore put
together a slideshow and two videos, available via this comment (Hopkins, 2018). One of the slides is included below,
with an explanatory paragraph. ·
Soon
after publication of this version, someone raised the concern that MBI could
be viewed as promoting unethically underpowered studies. We have therefore
amended the paragraph
about small samples. Magnitude-based inference (MBI) is an approach to making a
decision about the true or population value of an effect statistic, taking
into account the uncertainty in the magnitude of the statistic provided by a
sample of the population. In response to concerns about error rates with the
decision process (Welsh
and Knight, 2015), we
recently showed that MBI is superior to the traditional approach to
inference, null-hypothesis significance testing (NHST) (Hopkins and Batterham, 2016).
Specifically, the error rates are comparable and often lower than those of
NHST, the publishability rates with small samples are higher, and the potential
for publication bias is negligible. A statistician from Stanford University, Kristin Sainani, has
now attempted to refute our claims about the superiority of MBI to NHST (Sainani, 2018). We
acknowledge the effort expended in her detailed scrutiny and welcome the
opportunity to discuss the points raised in the spirit of furthering
understanding. Sainani argues that MBI should not be used, and that we should
instead "adopt a fully Bayesian analysis" or merely interpret the
standard confidence interval as a plausible range of effect magnitudes
consistent with the data and model. We have no objection to researchers using
either of these two approaches, if they so wish. Nevertheless, we have shown
before and show here again that MBI is a valid, robust approach that has
earned its place in the statistical toolbox. The title of Sainani's critique refers to "the
problem" with magnitude-based inference (MBI), but in the abstract she
claims that there are several problems with the Type-I and Type-II error
rates. In the article itself, she begins her synopsis of MBI with another
apparent problem: that the probabilistic statements in MBI about the
magnitude of the true effect are invalid. Throughout the critique are
numerous inconsistencies and mistakes. We solve here all her perceived
problems, highlight her inconsistencies and correct her mistakes. Should researchers make probabilistic assertions about the true
(population) value of effects? Absolutely, especially for clinically
important effects, where implementation of a possibly beneficial effect in a
clinical or other applied setting carries with it the risk of harm. We use
the term risk of harm to refer to
the probability that the true or population mean effect has the opposite of
the intended benefit, such as an impairment rather than an enhancement of a
measure of health or performance. It does not refer to risk of harm in a
given individual, which requires consideration of individual differences or
responses, nor does it refer to risk of harmful side effects, which requires
a different analysis. Magnitude-based inference is up-front with the chances
of benefit and the risk of harm for clinical effects, and the chances of
trivial and substantial magnitudes for non-clinical effects. This feature is
perhaps the greatest strength of MBI. Sainani states early on that "I
completely agree with and applaud" the approach of interpreting the
range of magnitudes of an effect represented by its upper and lower
confidence limit, when reaching a decision about a clinically important
effect. But, according to Sainani, "where Hopkins and Batterham's method
breaks down is when they go beyond simply making qualitative judgments like
this and advocate translating confidence intervals into probabilistic
statements, such as the effect of the supplement is 'very likely trivial' or
'likely beneficial.' This requires interpreting confidence intervals
incorrectly, as if they were Bayesian credible intervals." We have
addressed this concern previously (Hopkins and Batterham, 2016). The
usual confidence interval is congruent with a Bayesian credibility interval
with a minimally informative prior (Burton, 1994; Burton et al.,
1998; Spiegelhalter et al., 2004). As
such, it is an objective estimate of the likely range of the true value, and
the associated probabilistic statements of MBI are Bayesian posterior
probabilities with a minimally informative prior. The post-publication comments of
Little (2018) and
Lakens (2018) further
underscore this point. Unfortunately, full Bayesians disown us, because we prefer not
to turn belief into an informative subjective prior. Meanwhile, NHST-trained
statisticians disown us, because we do not test hypotheses. MBI is therefore
well placed to be a practical haven between a Bayesian rock and an NHST hard
place. (Others have attempted hybrids of Bayes and NHST, albeit with
different goals. See the technical notes.) From Bayesians we adapt valid
probabilistic statements about the true effect, based on the minimally
informative dispersed uniform prior. From frequentists (advocates of NHST) we
adapted straightforward computational methods and assumptions, and we
computed error rates for decisions based not on the null hypothesis but on
sufficiently low or high probabilities for the qualitative magnitude of the
true effect. The name magnitude-based
inference therefore seems justifiable, but in the Methods sections of
manuscripts, authors could or should note that it is a legitimate form of
Bayesian inference with the minimally informative dispersed uniform prior,
citing the present article. The appropriate reference for the decision
probabilities is the progressive statistics article in Medicine and Science in Sports and Exercise (2009).
Whether the resulting error rates are acceptable is an issue we will address
shortly. There is a logical inconsistency in Sainani's "qualitative
judgment" of confidence intervals. In her view, it is not appropriate to
make a probabilistic assertion about the true magnitude of the effect, but it
is appropriate to interpret the magnitude of the lower and upper confidence
limits. The problem with this approach is that it all depends on the level of
the confidence interval, so she is in fact making a quantitative judgment. Indeed, such judgments are actually
nothing more or less than magnitude-based inference, the only difference
being the width of the confidence interval. Towards the end of her critique
she cites "an excellent reference on how to interpret confidence
intervals (Curran-Everett, 2009)."
Here is a quote from that article: "A confidence interval is a
range that we expect, with some level of confidence, to include the
true value of a population parameter… a confidence interval focuses our
attention on the scientific importance of some experimental result." In
the three examples he gives, Curran-Everett states that the true effect is
"probably" within the confidence interval or "could
range" from the lower to the upper confidence limit. Again, this
interpretation is quantitative, with probably
and could defined by the level of
confidence of the confidence interval. There is a further inconsistency with Sainani's applause for
qualitative judgments based on the confidence interval: the fact that her
concerns about error rates in MBI would apply to such judgments. Consider,
for example, a confidence interval that overlaps trivial and substantial
magnitudes. What is her qualitative judgment? The effect could be trivial or
substantial, of course. Where is the error in that pronouncement? If the true
effect is trivial, we say there is none, but she says there is an
unacceptable ill-defined Type-I error rate. The only way she can keep a
well-defined NHST Type-I error rate is to make a qualitative judgment only if the effect is significant. In
other words, if the confidence interval does not overlap the null, she can
say that the effect could be trivial or substantial, but if it does overlap
the null, however slightly, she cannot say that it could be trivial.
Presumably she will instead call the magnitude unclear. If that is the process of qualitative judgment she has
in mind, it is obviously unrealistic. Sainani is also inconsistent when she makes the following
statement: "Hopkins and Batterham's logic is that as long as you
acknowledge even a small chance (5-25%) that the effect might be trivial when
it is [truly trivial], then you haven't made a Type I error… But this seems
specious. Is concluding that an effect is 'likely' positive really an
error-free conclusion when the effect is in fact trivial?" Consider the
confidence-interval equivalent of Sainani's statement. A small chance that
the effect could be trivial corresponds to a confidence interval covering
mostly substantial values, with a slight overlap into trivial values, such
that the probability of a trivial true effect is only 6%, for example. Hence
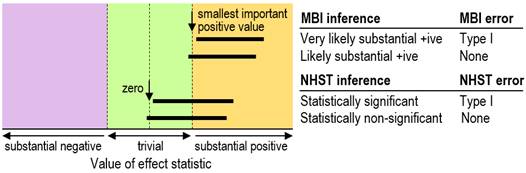
we say the effect could be trivial, so no Type-I error occurs (Figure 1).
Now consider what happens in NHST. If the 95% confidence
interval overlaps the null only slightly, with p=0.06, then a Type-I error
has not occurred (Figure 1). In other words, it's the same kind of decision
process as for MBI, except that in MBI the null is replaced with the smallest
important effect. The same argument could be mounted for Type-II errors:
Sainani does not specifically call our logic here specious, but she does show
later that our definitions "wildly underestimate" the traditional
Type-II error rates. We will not be held accountable for error rates based on
the null hypothesis. Sainani offers a novel solution to her perceived problem with
the definition of MBI Type-I error: allow for "degrees of error",
which inevitably makes higher Type-I error rates. But a similar inflation of
error rates would occur with NHST, if degrees of error were assigned to p
values that approach significance. We doubt if her solution would solve the
problems of the p value that are increasingly voiced in the literature; in
any case, we do not see the need for it with MBI. When an effect is possibly
trivial and possibly substantially positive, that is what the researcher has
found: it's on the way to being substantially positive. Furthermore, for
effects with true values that are close to the smallest important effect, the
outcome with even very large sample sizes will usually be possibly trivial and possibly substantial. Importantly, a
Bayesian analysis with any reasonable prior would reach this same conclusion,
because the prior is inconsequential with a sufficiently large sample size (Gelman et al., 2014). Now,
should such a finding be published? Of course, but we advise against making
inferences with the p value alone, because it will be <0.0001 and leave
the reader convinced that there is a substantial effect. It follows that such
outcomes with more modest sample sizes should also be published. By making a
clear possible outcome a publishable quantum, you also avoid substantial
publication bias, because researchers get more of their previously
underpowered studies into print with MBI. Adoption of MBI by the research
community would not result in a chaos of publication bias. On the contrary,
there would be negligible publication bias, and the farcical binary division
of results into statistically significant and non-significant at some
arbitrary bright-line p-value threshold would be consigned, along with the
null hypothesis, to the dustbin of failed paradigms. For researchers, reviewers and journal
editors who are still undecided about using MBI in preference to p values,
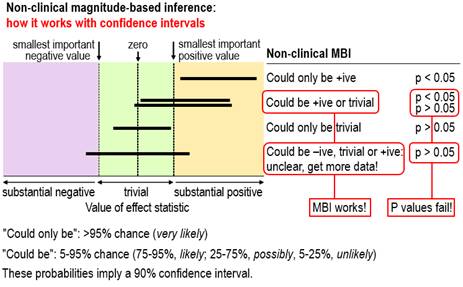
see Figure 2, which is taken from the slideshow and second video, available
via this comment. The figure shows outcomes with small
samples where the interpretation of the magnitude of the confidence
limits–that is, MBI–provides a succinct and accurate description of the
uncertainty in the magnitude of the true effect, whereas p values fail. For
the two outcomes where the conclusion with non-clinical MBI is could be +ive or trivial, one is
significant and the researcher would conclude there is an effect, while the other is non-significant and the
researcher would conclude there is no
effect. Both conclusions based on
the p value are obviously wrong; the conclusion with MBI properly describes
the uncertainty. For the outcome where the MBI conclusion is unclear, the p
value again fails, because non-significance would be interpreted as no effect, which does not represent
the fact that the true value could be substantially negative, trivial or
substantially positive. We have given the conventional
NHST interpretations of significance and non-significance here; the
interpretations of what we called conservative
NHST, according to which the magnitude only of significant effects can be
interpreted (Hopkins and Batterham, 2016), fare
little better.
Turning now to the problem of error rates in MBI, we find some
agreement and some disagreement with Sainani about the definitions of error.
We consider that we made a breakthrough with our definitions, because they
focus on trivial and substantial magnitudes rather than the null. As we
stated in our Sports Medicine article (Hopkins and Batterham, 2016), a
valid head-to-head comparison of NHST and MBI requires definitions of Type-I
(false-positive) and Type-II (false-negative) error rates that can be applied
to both approaches. In the traditional definition of a Type-I error, a truly
null effect turns out to be statistically significant. Sample-size estimation
in NHST is all about getting significance for substantial effects, so we
argued that a Type-I error must also occur when any truly trivial effect is declared
significant. It was then a logical step to declare a Type-I error in any
system of inference when a truly trivial effect is declared substantial. Sainani appears to have
accepted this definition. However, she seems unable to accept our definition
of a Type-II error. In our definition, a Type-II error occurs when a true
substantial effect is declared either trivial or substantial of opposite
sign. It's a false-negative error, in the sense that you have failed to infer
the effect's true substantial magnitude and sign. This definition makes good
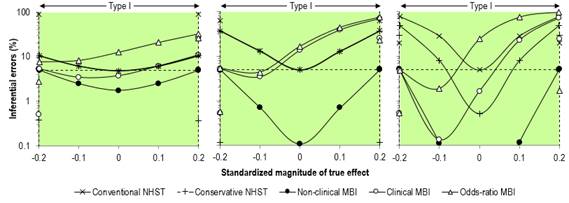
sense, especially when you consider a figure showing error rates on the Y
axis and true effects on the X axis (Figure 3). In her opening statement on definitions of error, Sainani states
that "Hopkins and Batterham are confused about what to call cases in
which there is a true non-trivial effect, but an inference is made in the
wrong direction (i.e., inferring that a beneficial effect is harmful or that
a harmful effect is beneficial). In the text, they switch between calling
these Type I and Type II errors." Yes, we may have caused confusion with
the following statement: "…implementation of a harmful effect
represents a more serious error than failure to implement a beneficial effect.
Although these two kinds of error are both false-negative type II errors,
they are analogous to the statistical type I and II errors of NHST, so they
are denoted as clinical type I and type II errors, respectively." They
are denoted as clinical Type-I and Type-II errors in the spreadsheet for
sample-size estimation at the Sportscience site, but they are correctly
identified as Type-II errors in our figure defining the errors, in the text
earlier in the article, and in the figures summarizing error rates. Sainani
goes on to state that "in their calculations, they treat them both as
Type II errors (Table 1a). But they can't both be Type II errors at the same
time." We do not understand this assertion, or her justification of it
involving one-tailed tests (but see the technical notes). She concludes with
"inferring that a beneficial effect is harmful is a Type II error,"
with which we agree, "whereas inferring that a harmful effect is
beneficial is a Type I error," with which we disagree. When a true
harmful effect is inferred not to be harmful, it is a Type-II error. Sainani
also notes that a true substantial effect inferred to be substantial of
opposite sign can be called a Type-III error, but we see no need for this
additional complication. That said, we do see the need to control the error
rate when truly harmful effects are inferred to be potentially beneficial.
Our rebuttal of Sainani's assertions about error rates might not
satisfy fundamentalist adherents of NHST. Figure 3 shows our original figure
from the Sports Medicine article and an enlargement of the Type-I rates. We
did not misrepresent these rates in the text, but arguably we presented them
in a manner that favored MBI: "For null and positive trivial values, the
type I rates for clinical MBI exceeded those for NHST for a sample size of
50+50 (~15–70 % versus ~5–40 %), while for the largest sample size, the type
I rates for clinical MBI (~2–75 %) were intermediate between those of
conservative NHST (~0.5–50 %) and conventional NHST (5–80 %)." These
error rates are consistent with those presented by Sainani, but the changes
of scale for the different true-effect magnitudes in her figure gives an
unfavorable impression of the MBI rates. We gave an honest account of the higher Type-I error rates with
odds-ratio MBI, which Sainani did not address. Our justification for keeping
this version of MBI in the statistical toolbox along with clinical MBI seems
reasonable. From the Sports Medicine article: "The Type-I rates for
clinical MBI were substantially higher than those for NHST for null and
positive true values with a sample size of 50+50. The probabilistic
inferences for the majority of these errors were only possibly beneficial, so
a clinician would make the decision to use a treatment based on the effect,
knowing that there was not a high probability of benefit. Type-I error rates
for odds-ratio MBI were the largest of all the inferential methods for null
and positive trivial effects, but for the most part these rates were due to
outcomes where the chance of benefit was rated unlikely or very unlikely, but
the risk of harm was so much lower that the odds ratio was >66. Inspection
of the confidence intervals for such effects would leave the clinician with
little expectation of benefit if the effect were implemented, so the high
Type-I error rates should not be regarded as a failing of this
approach." In her discussion, Sainani asserts: "Whereas standard
hypothesis testing has predictable Type I error rates, MBI has Type I error
rates that vary greatly depending on the sample size and choice of thresholds
for harm/benefit. This is problematic because unless researchers calculate
and report the Type I error for every application, this will always be hidden
to readers." But the "well-defined" Type-I rate for NHST is
only for the null; for trivial true effects it also varies widely with sample
size and choice of magnitude thresholds, and this variation is also hidden
from readers. The fact that the Type-I error rate for MBI peaks at the
optimum sample size (the minimum sample size for practically all outcomes to
be clear) is no cause for concern, because sample-size estimation in MBI is
based on controlling the Type-II rates. She goes on with this particularly
galling assertion: "Furthermore, the dependence on the thresholds for
harm/benefit makes it easy to game the system. A researcher could tweak these
values until they get an inference they like." This is a fatuous charge
to level against MBI. Any system of inference is open to abuse, if
researchers are so minded. A researcher who assesses the importance of
a statistically significant or non-significant outcome can choose the value
of the smallest important effect at that stage to suit the outcome obtained
with the sample. Researchers also game the NHST system by providing a justification
for sample size based on moderate effects. Sainani presumably has the same
concerns about full (subjective) Bayesians gaming not only the smallest
important effect but also the prior to get the most pleasing or publishable
outcome. Sainani's only remaining substantial concern about our
definition of error rates is not so easily dismissed. MBI provides a new
category of inferential outcome: unclear,
which is synonymous with unacceptably
uncertain, inadequately precise,
or perhaps most importantly, indecisive.
In our definition of Type-I and Type-II errors, you can't make an error until
you make a decision about the magnitude. The spreadsheets at the Sportscience
site (sportsci.org) state: "unclear; get more data." Hence we do
not include unclear as a Type-II
error when the true effect is substantial, or indeed as a Type-I error when
the true effect is trivial, a point that Sainani did not make. We applied
this definition even-handedly to what we call conservative NHST, where
researchers do not make a decision about an effect unless it is statistically
significant. A major outcome of our study of the various kinds of inference
is that the rates of decisive (and therefore publishable) effects for small
sample sizes with MBI are surpassed only by those with conventional NHST,
which is 100% decisive but pays for it with huge Type-II error rates. The
other major outcome is the trivial publication bias with MBI, whereas the
bias is substantial with NHST in both its forms. If the error rates with MBI
are as high as Sainani asserts, they obviously do not have implications for
publication bias. We have no hesitation about keeping indecisive outcomes out
of the rates of making wrong decisions, but if writing off MBI is on your
agenda, you will continue to assert that unclear outcomes are inferential
errors. Sainani concludes her critique with the following solution to fix what she regards as the MBI Type-I error problem: "…a one-sided null hypothesis test for benefit–interpreted alongside the corresponding confidence interval–would achieve most of the objectives of clinical MBI while properly controlling Type I error." We disagree. First, we do not wish to conduct "tests" of any kind; we embrace uncertainty and prefer estimation to "testimation", to borrow from Ziliak and McCloskey (2008). Secondly, the p value from her proposed one-sided test against the non-zero null given by the minimum clinically important difference is precisely equivalent to 1 minus the probability of benefit from MBI. If the one-sided test is conducted at a conventional 5% alpha level, the implication is that Sainani requires >95% chance of benefit to declare a treatment effective–equivalent to our very likely threshold. Elsewhere in her article, however, she suggests that "…clinical MBI should revert to a one-sided null hypothesis test with a significance level of 0.005." This test implies a requirement for a minimum probability of benefit of 0.995–equivalent to our most likely or almost certainly threshold. We regard both of these thresholds–and one-sided tests at 2.5% alpha favored in regulatory settings–as too conservative, particularly as clinicians and practitioners we have worked with over many years tell us that a 75% chance of benefit–or odds of 3:1 in favor of an intervention–is a cognitive tipping point for decision-making in the absence of substantial risk of harm. We also acknowledge that caution is warranted in making definitive inferences or decisions on the basis of a single study, but this is perhaps less of a problem, if the single study is a large definitive trial with a resulting precise estimate of treatment effect (Glasziou et al., 2010). Before we leave the issue of error rates, it is important to
note that the theoretical basis of NHST is now held to be untrustworthy by
some highly cited establishment statisticians. Consider, for example, the
following comments of two contributors to the American Statistical
Association's policy statement on p values (Wasserstein and Lazar, 2016; see the supplement):
"we should advise today’s students of statistics that they should avoid
statistical significance testing (Ken Rothman)" and "hypothesis
testing as a concept is perhaps the root cause of the problem (Roderick
Little)." If they are right, it follows that the traditional definitions
of Type-I and Type-II errors, both of which are based on the null hypothesis,
are themselves unrealistic and untrustworthy. Our definitions deserve more
recognition as a possible way forward. In her criticisms of the theory of MBI, Sainani claims that the
three references we cited in our Sports Medicine
article to support the sound theoretical
basis of MBI "do not provide such
evidence." We will now show that her claim is misleading
or incorrect for all three references. The first reference is Gurrin et al. (2000), from
which she quotes correctly: "Although the use of a uniform prior
probability distribution provides a neat introduction to the Bayesian
process, there are a number of reasons why the uniform prior distribution
does not provide the foundation on which to base a bold new theory of
statistical analysis!" However, she neglects to point out that later in
the same article Gurrin et al. make this statement: "One of the problems
with Bayesian analysis is that it is often a non-trivial problem to combine
the prior information and the current data to produce the posterior
distribution… The congruence between conventional confidence intervals and
Bayesian credible intervals generated using a uniform prior distribution
does, however, provide a simple way to obtain inferences in Bayesian form
which can be implemented using standard software based on the results and
output of a conventional statistical analysis… Our approach [effectively MBI]
is straightforward to implement, offers the potential to describe the results
of conventional analyses in a manner that is more easily understood, and leads naturally to rational decisions
[our italics]." Her claim about this reference is therefore misleading
and by omission, wrong. The second reference supporting MBI is Shakespeare et al. (2001).
Sainani states that this article "just provides general information on
confidence intervals, and does not address anything directly related to
MBI." On this point she is also wrong. The method presented by
Shakespeare et al. to derive what they refer to as "confidence
levels" uses precisely the same methods as MBI to derive the probability
of benefit beyond a threshold for the minimum clinically important difference.
For example, the authors present the following re-analysis of a previously
published study using their method: "The study found a survival benefit
of 28% favoring immediate nodal dissection (hazard ratio 0·72, 95% CI
0·49–1·04). There is a… 94% level of confidence [i.e., chance of benefit]
that the survival benefit is clinically relevant (improvement in survival of
3% or more). The information contained
in confidence levels is clearly far more useful than CIs alone to clinicians
in applying results to daily practice [our italics]." This method is
very obviously MBI in all but name. Shakespeare et al. also calculated the
risk of harm, but it was the risk of harmful side effects, not the risk of the opposite of a beneficial
outcome. The third reference that she claims does not provide evidence
supporting MBI is our letter to the editor (Batterham and Hopkins, 2015) in
response to the article by Welsh and Knight (2015). By her
account, this reference "is a short letter in which they point to
empirical evidence from a simulation that I believe is a preliminary version
of the simulations reported in Sports Science [sic]." But the issue here
is the theoretical basis of MBI, which indeed we had argued succinctly in the
letter. Hence this claim also is wrong. Finally, the overarching negative tone of Sainani's critique
deserves attention. We counted three occasions in the article where she gives
any credit to our achievement with MBI, but each is immediately followed by
an assertion that we were misguided or mistaken. She is the one who is
misguided or mistaken. It is deeply disappointing and discouraging when
someone in her position of influence fails to notice or acknowledge the
following novel contributions that
we have made to the theory and practice of inference: the definitions of
inferential error that go beyond the null (nil) hypothesis and statistical significance;
sample-size estimation based on controlling these errors, especially the risk
of declaring a harmful effect potentially implementable; the higher
publishability rates and negligible publication bias with MBI compared with
NHST; quantitative ranges for qualitative measures of probability; smallest
and other magnitude thresholds for the full range of effect statistics in the
sports-medicine and exercise-science disciplines; procedures for estimating
and assessing the magnitude of the standard deviation representing individual
responses with continuous outcomes and of the moderators explaining them; the
need for a distinction between clinical and non-clinical inference; the
concept of clear effects with the
two kinds of inference, and the associated decision rules based on adequate
precision or acceptable uncertainty; and easily the most valuable of all, the
notion of accounting for the risk of harm–the probability that the true
effect represents impairment rather than enhancement of health or performance–with
clinically important effects. There is still room for debate that
could result in improvements in MBI. The most obvious debatable feature are
the rules we have devised for deciding when effects are clear in clinical and
non-clinical settings–in other words, the rules for acceptable uncertainty in
the two settings. These rules in turn depend on the threshold probabilities
that define the terms most unlikely,
very unlikely, unlikely, possible, likely, very likely and most likely, because it is only with
these or similar qualitative terms that researchers, clinicians and
practitioners can make informed decisions as stakeholders. The decision must
not be left solely with the statisticians. Some will argue that these
thresholds are as arbitrary as the p value of 0.05 defining significance. Our
rejoinder is that our thresholds are for real-world probabilities based on
experience with clinicians and practitioners. They are also similar to, and a
little more conservative than, those used by the Intergovernmental Panel on
Climate Change (Mastrandrea et al., 2010),
another group of scientists who are concerned about communicating decisions
based on plain-language probabilities of outcomes. Furthermore, our
simulations showed that they provide realistic publication rates and
negligible publication bias for small-sample research. Anyone wishing to
define clear more conservatively
will inevitably reduce publication rates and increase publication bias. We have demonstrated that the error rates in MBI are acceptable overall. However, those wishing to use MBI, but who remain concerned with error rates, could present an additional statistic with excellent error control, the second-generation p-value (SGPV) (Blume et al., 2018). Briefly, this statistic is based on an interval null hypothesis equivalent to the trivial region in MBI. The SGPV is not a probability; rather it is the proportion of hypotheses supported by the data and model that are trivial. If the SGPV=0, then the data support only clinically meaningful hypotheses. If the SGPV=1, then the data support only trivial hypotheses. Values between 0 and 1 reflect the degree of support for clinically meaningful or trivial hypotheses, with a SGPV of 0.5 indicating that the data are strictly inconclusive. If the attack on MBI results in
journal editors banning the use of MBI in submitted manuscripts, and if the
editors do not accept MBI as reference
Bayesian analysis with a dispersed uniform prior, what is the
alternative? We have shown that simple presentation of the confidence
interval is effectively MBI, and that hypothesis tests against the smallest
important effect are far too conservative. Researchers may therefore have to
make the choice between Bayesian analysis with informative priors and a return to p values. We have argued in a comment
(Hopkins and Batterham, 2018) that
full Bayesian analyses are generally unrealistic and challenging for most
researchers, which leaves p values as Hobson's choice for researchers and a
stop-gap choice for reviewers and editors. In the same comment, we pointed
out the following two unfortunate consequences. First, many small-scale
studies with clear outcomes in MBI will no longer be publishable, because the
outcomes will not be significant. These effects, which do not suffer from
substantial bias, will no longer contribute to meta-analyses, where they
would have helped push the overall sample size up to something that gives
definitive outcomes. Meta-analyses based on a large number of small studies
rather than a few large studies also give better estimates of the modifying
effects of study and subject characteristics and thereby better
generalizability to more settings. Secondly, it will be harder for research
students to get publications, because they will need larger sample sizes to
get significance, often impractically large when the subjects are competitive
athletes. Their careers will therefore suffer needlessly. The lack of substantial bias with
MBI should not be used as an excuse for performing underpowered studies. In
the simulations of controlled trials where the MBI-optimal sample size was 50
in each group, a sample size of 10 in each group resulted in ~55-65% unclear
non-clinical effects and ~20-65% unclear clinical effects over the range of
true trivial effects (Hopkins and Batterham, 2016). It is
unethical to undertake research when the expectation of a decisive outcome
for trivial effects is determined by a coin toss, but when an optimal sample
size for trivial effects is not possible, should the research should still be
performed? Yes, if there is a genuine expectation that the effect will have
sufficient magnitude to be clear, or if another cohort of participants can be
recruited eventually to make the sample size adequate (although the bias with
a group-sequential design in MBI has yet to be investigated). The smaller
sample sizes for publishability with MBI reduce the risk of unethically underpowered
studies compared with NHST. In conclusion, MBI represents a trustworthy mechanism for
representing the uncertainty in effects with well-defined qualitative
categories of probability. It beggars belief that any journal reviewer or
editor could take exception to publication of an effect as being harmful, trivial, beneficial, substantial
increase, or substantial decrease
prefaced by possibly, likely, very
likely, or most likely. Such
outcomes, along with unclear,
should be welcomed as a sunny spring following a long dark winter of p-value
discontent. Instead, MBI has now experienced two one-sided negative
critiques. The current critique turns largely on the assertion that possibly beneficial outcomes in
clinical MBI and unlikely trivial
and possibly trivial outcomes in
non-clinical MBI have unacceptably high Type-I error rates. We have shown
that the error rates are generally lower than those of NHST, and where any
are high, they are comparable with those of NHST. By communicating the
uncertainty in the magnitude of effects in plain language, by increasing the
rates of publishability, and by eliminating the potential for publication
bias, MBI has provided a valuable service to the research community. A return
to hypothesis testing, p values and statistical significance is unthinkable.
MBI should be used. Acknowledgments: Thanks to Steve Marshall, Ken Quarrie and Fabio Serpiello, who provided useful feedback on drafts. Thanks also to those who responded with the published comments, and to colleagues at Victoria University (Fabio Serpiello, Steph Blair, Luca Oppici, and Craig Pickett), who provided feedback on the slideshow/videos, and to Ken Quarrie, who provided the Sainani-style error graphics therein. Technical notes
Throughout
this article, null means nil or zero, rather than Fisher's generic conception of the hypothesis
to be nullified (Cohen, 1994). We
make this point, because some have argued that, instead of MBI or full
Bayesian inference, one could perform a hypothesis test against the minimum
important difference, rather than against the nil hypothesis, and present a p
value for that test (e.g., Greenland et
al., 2016).
Sainani may have had this in mind when she wrote: "In addition, a
one-sided null hypothesis test for benefit–interpreted alongside the
corresponding confidence interval–would achieve most of the objectives of
clinical MBI while properly controlling Type I error." Here, by null she presumably means the hypothesis to be nullified: the
smallest important beneficial effect. Some
full Bayesians have previously taken exception to the non-informative or
"flat" prior of MBI, by invoking two arguments. First, representing
such a prior mathematically is an intractable problem (Barker and Schofield, 2008). We
delighted in parodying this argument by calling the flat prior an imaginary
Bayesian monster (Hopkins and
Batterham, 2010): the
argument is easily dismissed simply by making the prior minimally
informative, which makes the prior tractable but makes no substantial
difference to the posterior. The second argument is that a uniform flat or
minimally informative prior must become non-uniform, if the dependent
variable is transformed, for example using logarithms or any of the
transformations in generalized linear modeling (e.g., Gurrin et al., 2000). Again,
this argument is easily dismissed: the flat or minimally informative prior is
applied to the transformation of the dependent variable in a model that makes
least non-uniformity of the effect and error compared with any other
transformations (including non-transformation) and models. What happens to
the prior with these other transformations and models is irrelevant. Interestingly,
if we were full Bayesians, we might not be expected to concern ourselves with
error control, as some full Bayesians distinguish "beliefs" from
estimates of "true" values; for them, frequentist notions such as
Type-I errors do not exist (Ventz and Trippa, 2015). A full
Bayesian–with the caveat that more than 30 years ago there were already
46,656 kinds (Good, 1982)–might
say, for example, that "75% of the credible values exceed the minimum
clinically important threshold for benefit”, whereas the MBI exponent would
claim that "the probability that the true value of the treatment exceeds
the threshold for benefit is 75%; that is, the treatment is likely
beneficial." In MBI, adopting a least-informative prior and making
decisions based on a posterior distribution equivalent to the likelihood
arguably requires us to give due consideration to error control, which we
have done. The general notion of Bayesian inference with a model chosen to
yield inferences with good frequency properties has been described as
"Calibrated Bayes" (Little, 2011; Little, 2006). Other
attempts at reconciling Bayesian and frequentist paradigms include
"Constrained Optimal Bayesian" designs (Ventz and Trippa, 2015). Meanwhile, to make probabilistic statements, Sainani
recommends we adopt a full Bayesian analysis, in which there is no apparent
requirement for error control, while lambasting MBI for having higher error
rates in some scenarios. Her position once again is inconsistent. References
Cohen J (1994). The earth is round (p < .05). American Psychologist 49, 997-1003 Mastrandrea MD, Field CB, Stocker TF, Edenhofer O, Ebi KL, Frame DJ, Held H, Kriegler E, Mach KJ, Matschoss PR, Plattner G-K, Yohe GW, Zwiers FW (2010). Guidance Note for Lead Authors of the IPCC Fifth Assessment Report on Consistent Treatment of Uncertainties. Intergovernmental Panel on Climate Change (IPCC): https://www.ipcc.ch/pdf/supporting-material/uncertainty-guidance-note.pdf Draft 2 published
14 May 2018. |