Competitive Performance of Elite Track-and-Field Athletes: Variability and Smallest Worthwhile Enhancements Will G Hopkins Sportscience 9, 17-20, 2005 (sportsci.org/jour/05/wghtrack.htm)
|
|
Effect of Time
between Competitions IntroductionThis paper is the latest in a series aimed at estimating the smallest worthwhile change in performance for athletes who compete as individuals in sports where the outcome is determined by a single score, such as a time or distance. The smallest worthwhile change in performance is important when assessing athletes with a performance test to make decisions about meaningful changes in an individual or to research strategies that might affect performance (Hopkins, 2004). An estimate of the smallest change comes from an analysis of reliability (reproducibility or variability) of competitive performancethe smallest change is in fact about half the typical variation a top athlete shows from competition to competition (Hopkins et al., 1999). The previous published studies on variability of competitive performance and smallest changes have been for junior swimmers (Stewart and Hopkins, 2000), elite swimmers (Pyne et al., 2004), non-elite runners (Hopkins and Hewson, 2001), and triathletes (Paton and Hopkins, 2005). The present study of track-and-field athletes is based on data that I acquired and analyzed some years ago and that I have referred to in various publications. MethodsOfficial
result times of the 1997 Grand Prix series of international competitions were
obtained from the website of the International Amateur Athletic Federation.
The series consisted of 18 different kinds of track-and-field events staged
at 17 mainly European venues over 101 days. An event at a venue was included
in the analysis of reliability for that kind of event if it included at least
2 athletes who had entered the same event at other venues. The men's high jump provided the least
amount of data: 8 athlete-entries for
3 athletes at 3 venues; at the other extreme, the men's 110-m hurdle provided
120 athlete-entries for 20 athletes at 17 venues. A typical women's event in the analysis was
the javelin, which provided 48 athlete-entries for 12 athletes at 7
venues. There were insufficient data
for the analysis of hammer throw, women's long jump and women's pole vault. The
analyses were similar to those used in the study of triathlete performance in
this issue (Paton and Hopkins, 2005). Briefly, I used mixed modeling of
log-transformed times to derive an athlete's typical percent variation in performance
from competition to competition as a coefficient of variation. I performed separate analyses for males and
females in each event, and for the top and bottom half of athletes in each
event. Differences between
coefficients of variation were considered substantial if their ratio was
greater than 1.10. I also
analyzed for the effect of time on variability estimated between all pairs of
competitions for both sexes combined but for shorter (100- to 1500-m) and
longer (3000- to 10,000-m) running events separately. I corrected the small bias in the
individual estimates of coefficients of variation by multiplying by
1+1/(4DF), where DF=degrees of freedom (Gurland and Tripathi, 1971). I then fit quadratics to the log-log plots
and used 1000 bootstrapped samples to derive confidence limits for the
quadratics and for comparisons (ratios) of the coefficients of variation for
different times between competitions. Results and DiscussionEffect of EventTable
1 shows the typical within-athlete variation in performance from competition
to competition for the various events. I have not systematically derived confidence
limits for a comparison of the variability in the different types of event,
but it is reasonably clear from the confidence limits for each type that
athletes in longer running events are more variable their performance than
those in the shorter events, that athletes in the throwing events are about
twice as variable, and that athletes in the high jump and triple jump are somewhere
in between.
The higher reliability of the shorter
running and hurdling events may be due to differing contributions of energy
systems, pacing strategies, and wind resistance relative to the longer
events. Contributions of energy
systems and skill may explain the lower reliability of field events and differences
between the field events. The
differences between variability of performance in the different types of
event mirrors those in performance tests in these modes of exercise (Hopkins et al., 2001), although the variability in
these competitions is generally a little less than that for athletes in the
best tests. Effect of SexTable 2 shows the variability in performance for females and males in the events where there were sufficient comparable data. Given the uncertainty in the estimates of variability, females were probably more variable than males by a trivial-small factor of ~1.1 (about 10%) overall, but there may be greater or smaller differences in specific events. The difference may be due to less depth of competition for the females rather than differences in physiology.
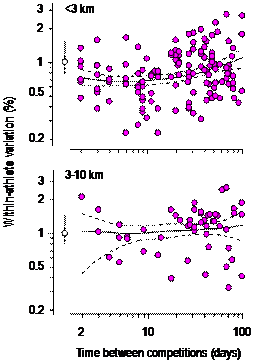
Effect of Time between CompetitionsThe estimates
of athlete variability in running and hurdling events for all pairwise
combinations of competitions are shown in Figure 1. Much of the scatter in the points is due to
sampling variation arising from the small sample size for the pairwise
combinations, as can be seen from the expected sampling variation for a
typical point.
Athlete
variability for short runs was minimum (0.7%) at around 1 wk between
competitions and greatest at 100 d (1.1%).
The trend towards more variability with increasing time between competitions
was clear: for example, the ratio of variability at 64 d to that at 8 d was
1.40 (90% confidence limits 1.161.65). The quadratic model probably
overestimates the trend for longer times, because a plateau is evident in the
plot beyond ~50 d. A small increase in variability due to variation in training
and health over a period of weeks is not unexpected, but over more than
several months these athletes, like elite triathletes (Paton and Hopkins, 2005), probably maintain their
ability to perform. Variability
for the long runs was also a minimum (1.0%) around 1 wk between competitions
for this sample. However, confidence
limits were too wide to allow conclusions about any substantial trend; for
example, the ratio of 100-d to 8-d variability was 1.16 (0.771.69).
Effect of Caliber of AthleteTable 3 shows that the athletes in the top half of the field were clearly less variable in the running events. Others have found similar results with running and swimming and cycling and have attributed it to better pacing, more consistent preparation, or more consistent motivation on the part of the very best athletes (Hopkins and Hewson, 2001; Stewart and Hopkins, 2001; Pyne et al., 2004; Paton and Hopkins, 2005). I favor the last of these possible explanations for endurance athletes: an athlete who realizes early on that s/he is not in the medal stakes must surely sometimes put less effort into the rest of the race. The situation is less clear in the field events, owing to the uncertainty in the estimates. More data are required before one seeks explanations for what may be more variability with top-half athletes in the throwing events. ConclusionsThe main purpose of this study was to obtain estimates of the smallest worthwhile change in performance for elite athletes in each of the track-and-field events. Halving the variability of performance of the best athletes in each event provides such estimates. Coaches and sport scientists should therefore focus on enhancements of as little as 0.3-0.5% for elite track athletes through 0.9-1.5% for elite field athletes. ReferencesGurland J, Tripathi RC (1971). A simple
approximation for unbiased estimation of the standard deviation. American
Statistician 25(4), 30-32 Hopkins WG (2004). How to interpret changes in an athletic
performance test. Sportscience 8, 1-7 Hopkins WG, Hawley JA, Burke LM (1999). Design and analysis of
research on sport performance enhancement. Medicine and Science in Sports and
Exercise 31, 472-485 Hopkins WG, Hewson DJ (2001). Variability of competitive performance
of distance runners. Medicine and Science in Sports and Exercise 33,
1588-1592 Hopkins WG, Schabort EJ, Hawley JA (2001). Reliability of power in
physical performance tests. Sports Medicine 31, 211-234 Paton CD, Hopkins WG (2005). Competitive performance of elite
Olympic-distance triathletes: reliability and smallest worthwhile enhancement.
Sportscience 9, 1-5 Pyne D, Trewin C, Hopkins W (2004). Progression and variability of
competitive performance of Olympic swimmers. Journal of Sports Sciences 22,
613-620 Stewart AM, Hopkins WG (2000). Consistency of swimming performance
within and between competitions. Medicine and Science in Sports and Exercise
32, 997-1001 Stewart AM, Hopkins WG (2001). Seasonal training and performance of
competitive swimmers. Journal of Sports Sciences 18, 873-884 Published Dec 2005 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||