|
A New View of Statistics |
© 2002 Will G Hopkins |
![]() A Scale of Magnitudes for Effect
Statistics
A Scale of Magnitudes for Effect
Statistics
Correlations
Jacob Cohen has written the most on this topic. In his
well-known book he suggested, a little ambiguously, that a
correlation of 0.5 is large, 0.3 is moderate, and 0.1 is small
(Cohen, 1988). The usual interpretation of this
statement is that anything greater than 0.5 is large, 0.5-0.3 is
moderate, 0.3-0.1 is small, and anything smaller than 0.1 is
insubstantial, trivial, or otherwise not worth worrying about. His
corresponding thresholds for standardized differences in means are 0.8, 0.5
and 0.2. He did not provide thresholds for the relative risk and odds
ratio.
For me, the main justification for this scale of correlations comes from the interpretation of the correlation coefficient as the slope of the line between two variables when their standard deviations are the same. For example, if the correlation between height (X variable) and weight (Y variable) is 0.7, then individuals who differ in height by one standard deviation will on average differ in weight by only 0.7 of a standard deviation. So, for a correlation of 0.1, the change in Y is only one-tenth of the change in X. That seems a reasonable justification for calling 0.1 the smallest worthwhile correlation. I guess it's also reasonable to accept that a change in Y of one half that in X (corresponding to r = 0.5) is also the threshold for a large effect, and r = 0.3 seems a logical way to draw the line between small and moderate correlations.
Threshold values for standardized differences or changes in means and for relative frequency can be derived by converting these statistics to correlations. The procedure is a little artificial, so the resulting values need to be scrutinized to ensure they make sense. Here's how it's done.
Differences in Means
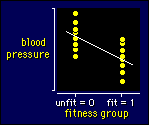 To work out a scale of magnitudes
for differences or changes in means, you need a dimensionless measure comparable to the correlation coefficient. The best and possibly only such measure is the standardized difference. Cohen used the letter d to represent the standardized difference, and it is often known as Cohen's d. To see how to get thresholds for d from those for correlations, let's introduce
a new predictor variable with the value of 0 for one group and 1 for the other,
as shown in this example for the effect of fitness on blood pressure. (We can
assign any number at all to each group, not just 0 and 1.) We then calculate
the correlation between this variable and the dependent variable. If the standardized difference between the means is d (the difference in the means divided by the standard deviation in either group, here assumed to be the same), it's possible to show from the definition of a correlation that r = d/√(d2+4), or rearranging, d = 2r/√(1-r2). It follows that
correlations of 0.1, 0.3, and 0.5 correspond to standardized differences in means of 0.20, 0.63,
and 1.15.
To work out a scale of magnitudes
for differences or changes in means, you need a dimensionless measure comparable to the correlation coefficient. The best and possibly only such measure is the standardized difference. Cohen used the letter d to represent the standardized difference, and it is often known as Cohen's d. To see how to get thresholds for d from those for correlations, let's introduce
a new predictor variable with the value of 0 for one group and 1 for the other,
as shown in this example for the effect of fitness on blood pressure. (We can
assign any number at all to each group, not just 0 and 1.) We then calculate
the correlation between this variable and the dependent variable. If the standardized difference between the means is d (the difference in the means divided by the standard deviation in either group, here assumed to be the same), it's possible to show from the definition of a correlation that r = d/√(d2+4), or rearranging, d = 2r/√(1-r2). It follows that
correlations of 0.1, 0.3, and 0.5 correspond to standardized differences in means of 0.20, 0.63,
and 1.15.
Problem! Cohen's thresholds for small, moderate and large are 0.20, 0.50 and 0.80. The lowest of these two sets of values agree (0.20), but the others don't. Cohen derived his thresholds from a consideration of non-overlap of the distributions of values in the two groups. He chose certain arbitrary amounts of non-overlap as defining his thresholds. The thresholds for small obviously correspond, but the others don't.
Something like Cohen's thresholds for standardized differences can be got by making the independent variable normally distributed, then "dichotomizing" it by splitting its values down the middle to make the two fitness groups. Correlations of 0.1, 0.3, and 0.5 then turn into standardized differences of 0.17, 0.50, and 0.87: yet another set of thresholds! Which set is correct? I think that this dichotomizing operation throws away information, and that therefore the values of 0.17, 0.50 and 0.87 underestimate the thresholds.
I'm happy to agree with Cohen that 0.20 is the threshold for smallest standardized differences in a mean. If we also assume that the thresholds of 0.1, 0.3 and 0.5 for correlations are acceptable, there is another approach to demonstrating that the other thresholds for standardized differences in the mean should be 0.63 and 1.15. Assume further that the X and Y variables are normally distributed. Consider first a correlation of 0.1. Imagine you are comparing two individuals with X values that differ by an amount a. They will, of course, have different Y values. From one of the meanings of the correlation coefficient, the difference in the Y values is a.r.SDy/SDx, where SDy and SDx are the standard deviations of the Y and X variables. To standardize this difference, we have to divide it by the appropriate standard deviation, which in this case is the standard error of the estimate, given by SDy√(1-r2). The standardized difference in the Y values is therefore a.r.SDy/SDx/(SDy√(1-r2)) = (a/SDx)(r/√(1-r2)). So, if we want a smallest correlation of 0.1 to be equivalent to a smallest standardized difference of 0.20 between two individuals, the individuals have to differ on average by 2 standard deviations of the X values: (2SDx/SDx)(0.1/√(1-0.12) = 0.20. It follows that the standardized difference corresponding to any correlation r should be the difference corresponding to 2 standard deviations of the X values, and the formula to convert a correlation to an equivalent standardized difference in the means is therefore 2r/√(1-r2). Note that this formula is the same as in the first paragraph of this section, so the thresholds for moderate and large are 0.63 and 1.15.
One reality check on these thresholds comes from considering the average separation between individuals in a normally distributed population. It turns out to be 1.13 standard deviations, which is a standardized difference of 1.13. So we have to ask: is it reasonable that the average difference between individuals in a population should be on the threshold between moderate and large? I think so, and I therefore think that Cohen's 0.5 and 0.8 are too low to define the thresholds for moderate and large effects.
Relative Frequencies
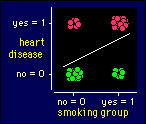 To work out a scale for comparing frequencies, we have to code
not only the grouping variable, but also the dependent variable. See the example
on the right, in which a cluster of points represents the frequencies for each
level of the independent and dependent variables. Once again the values of 0
and 1 for the variables don't matter, but if we represent the frequencies as
percents in each group, we get something really nice. For the example shown,
heart disease was 75% in the smoking group and 30% in the non-smoking group.
The difference in frequencies (75 - 30 = 45%) divided by
100 is 0.45, which turns out to be the correlation between our two newly coded
variables. This result--the correlation times 100 equals the difference in percent
frequencies--is true for all frequencies. The threshold correlations of 0.1,
0.3, and 0.5 therefore convert to thresholds of 10, 30 and 50 for differences
in percent frequencies between the occurrence of something in two groups.
To work out a scale for comparing frequencies, we have to code
not only the grouping variable, but also the dependent variable. See the example
on the right, in which a cluster of points represents the frequencies for each
level of the independent and dependent variables. Once again the values of 0
and 1 for the variables don't matter, but if we represent the frequencies as
percents in each group, we get something really nice. For the example shown,
heart disease was 75% in the smoking group and 30% in the non-smoking group.
The difference in frequencies (75 - 30 = 45%) divided by
100 is 0.45, which turns out to be the correlation between our two newly coded
variables. This result--the correlation times 100 equals the difference in percent
frequencies--is true for all frequencies. The threshold correlations of 0.1,
0.3, and 0.5 therefore convert to thresholds of 10, 30 and 50 for differences
in percent frequencies between the occurrence of something in two groups.
Now, are you happy with the notion that a difference of 10% in the frequency of something between two groups is indeed small? For example, if you made sedentary people active and thereby reduced the incidence of heart disease from 55% to 45% in some age group, would that be a small gain? At first glance you'd think this gain might be better described as moderate. Perhaps the way to view it is that the 10% in question is only one tenth of the entire group. On an absolute population basis, we may be talking about a lot of people, but it's still only one in 10. The threshold between moderate and large represents something that affects half the group, which seems OK. The boundary between small and moderate (three people in 10) is also acceptable.
Frequency differences do not convert simply into relative risks, because the values of this statistic depend on the frequencies in each group. For example, the threshold frequency difference of 10% for the smallest worthwhile effect represents a relative risk of 55/45 or 1.22 if the frequencies are 55% and 45%, but the relative risk is 11 if the frequencies are 11% and 1%. The odds ratio is even more sensitive to the absolute frequencies in each group. The smallest values for the relative risk and odds ratio occur when the frequencies in the two groups are symmetrically disposed about 50% (55-45, 60-40, 65-35 and so on).
The Complete Scale
It seems to me that the vista of large effects is left
unexplored by Cohen's scale. Surely more than just large can
be applied to the correlations that lie between 0.5 and 1? What's
missing from the picture is a rationale for breaking up this big half
of the scale with a couple more levels. Here's the way I do it:
|
|
trivial |
small |
moderate |
large |
large |
perfect |
| |||||||
|
Correlation |
|
|
|
|
|
|
| |||||||
|
Diff. in means |
|
|
|
|
|
|
| |||||||
|
Freq. diff. |
|
|
|
|
|
|
| |||||||
|
Rel. risk |
|
|
|
|
|
|
| |||||||
|
Odds ratio |
|
|
|
|
|
|
| |||||||
I've adopted a Likert-scale approach by using very for the level above large, and I've assigned it to a correlation of 0.7 to keep the scale linear for correlations and frequency differences. A level of magnitude above very large is warranted for correlations, because a value of 0.9 is a kind of threshold for validity when the associated straight line is used to rank individuals, and reliability needs to be greater than 0.9 to be most useful for reducing sample sizes in longitudinal studies. I've opted for nearly perfect to describe these correlations. Values for the other effect statistics were calculated as before, and the values for the relative risk and odds ratio are the minimum values for these statistics.
To finish, here is a graphical representation of the scale...
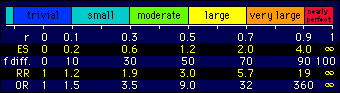
...and a table of synonyms for the descriptors (for simplicity, only for the correlation coefficient). Use of these synonyms shouldn't lead to any confusion about the magnitude of the effect:
|
Coefficient |
Descriptor |
|
|
trivial, very small, insubstantial, tiny, practically zero |
|
|
small, low, minor |
|
|
moderate, medium |
|
|
large, high, major |
|
|
very large, very high, huge |
|
|
nearly, practically, or almost: perfect, distinct, infinite |
SAS programs that generated the results on this page are
attached.
Other Effect Statistics
Cohen devised several other effect statistics and discussed
their magnitudes, but I have not seen these statistics in
publications. He also considered whether, for example,
variance explained (the
correlation squared) might be a more suitable scale to represent
magnitude of linearity, especially when you take into account the
useful additive property of variance explained in such things as
stepwise regression. He rejected
it, though, because a correlation of 0.1 corresponds to a variance
explained of only 1%, which he thought did not convey adequately the
magnitude of such a correlation. I agree.
The so-called common-language effect statistic (McGraw & Wong, 1992) or probability of superiority represents a more recent attempt on the summit of a universal scale of magnitudes. This statistic is easiest to understand when you compare two groups whose means differ. The probability of superiority is the probability that someone drawn at random from one group will have a higher value than someone drawn from the other group. The problem here is that no difference between the means implies a value of 50% or 0.5 (equal chance that the person will have a higher or lower value). A value of 50% for no difference doesn't feel right.
The next page starts a new topic, dimension reduction.
McGraw, K. O., & Wong, S. P. (1992). A
common language effect-size statistic. Psychological Bulletin, 111,
361-365.
Go to: Next · Previous · Contents · Search
· Home
Last updated 7 August 06