Bias in Bland-Altman but not Regression Validity Analyses Will G Hopkins Sportscience 8, 42-46, 2004
(sportsci.org/jour/04/wghbias.htm)
|
|
For comparison of one method with another, Bland and Altman (1986) advised researchers to use the two methods on a group of subjects, then plot the difference scores against the mean for each subject. Such plots have become a standard accessory in validity or method-comparison studies, and their original paper has been cited over 9000 times. In this article I use a spreadsheet to show that the plots can lead to an incorrect conclusion about the validity of a measure, and I urge researchers to use regression when comparing measures. Bland and Altman devised their plot to steer researchers away from what they considered was misuse of the correlation coefficient as a measure of validity. The misuse amounted to regarding the correlation coefficient as the most important or even the only measure of the relationship between two measures. The problem with the correlation coefficient is that the two measures might be highly correlated, yet there could be substantial differences in the two measures across their range of values. An appropriate comparison of the two measures needs to highlight such differences—hence the Bland-Altman plot, which explicitly shows differences between the two measures (on the Y axis) over their range (on the X axis). Unfortunately the Bland-Altman plot has a
fatal flaw: it indicates incorrectly that there are systematic differences or
bias in the relationship between two measures, when one has been
calibrated against the other. Whether
this flaw has been noted previously in any of the 9000+ citations to Bland
and Altman would be hard to determine.
There was no mention of it either in the most recent re-statement of
their method (Bland and Altman, 2003) or in a recent critique focused on bias (Ludbrook, 2002). I became aware of the problem at a
colloquium on measurement presented by Greg Atkinson and Alan Batterham at
the 2004 annual meeting of the The spreadsheet shows randomly generated data simulating a not uncommon scenario: calibration of an instrument against some standard or criterion, followed by a method-comparison study of the instrument against the criterion. For the calibration phase of the simulation, imagine that a manufacturer makes a new high-tech instrument to provide a practical measure of something like body fat, blood pressure, or transdermally assayed components of plasma. The instrument measures a biophysical parameter such as absorbance ("Practical X" in the spreadsheet) that is highly correlated with the variable of interest (the concentration of some substance in plasma, say), although it may not be in anything like the same units. So the manufacturer uses the instrument on a large sample of subjects and does a criterion measurement of the variable ("Criterion Y") on the same sample. The manufacturer then fits a prediction equation to make Practical X predict Criterion Y as closely as possible, and finally builds the equation into the instrument. The instrument therefore produces a calibrated practical measure ("Practical Y") that is outwardly like Criterion Y but will almost certainly have more error than the criterion.
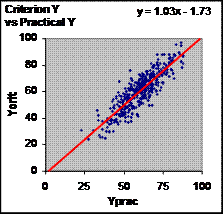
For the simulated method-comparison or validity phase, imagine that a researcher wants to use the instrument for a large-scale study. The researcher prudently decides to check the instrument against the criterion by measuring a sample of subjects with the instrument and with the criterion. Figure 1 shows the first stage of the analysis: a plot of raw values provided by the instrument and the criterion for 400 subjects. To generate these data, I made arbitrary choices for constants and errors in the manufacturer's calibration phase, but the conclusions about bias that I am about to make are independent of these choices. The conclusions are also independent of the sample size. I chose 400 to make variation in derived statistics from sample to sample negligible. In any real calibration and validity study, samples of 400 would be wasteful. Note that the slope of the line is close to unity, and the intercept of the line is close to zero. In fact, the expected values of these parameters are exactly 1 and 0, and they differ from their expected values only because of sampling variation. To demonstrate this variation, download the spreadsheet, open it, then save it by hitting the Control and "S" key. The spreadsheet updates all the randomly generated numbers with new values. In doing so, the spreadsheet will perform the manufacturer's calibration study with a new sample of 400 subjects, then perform the validity study with another new sample of 400 subjects. The slope and intercept vary randomly around 1 and 0 respectively with every save. A value of 1 for the slope and 0 for the intercept implies that the practical measure is unbiased. Measures of bias are only one aspect of a validity study. Equally important is the nature of the random error in measurements provided by the instrument. This error is apparent in the scatter of points about the line of identity in Figure 1. The magnitude of the error is usually calculated as the standard error of the estimate: the standard deviation of the vertical distance of each point from the line. The standard error of the estimate represents the typical magnitude of the deviation, error or difference (plus or minus) between the instrument's measurement and the criterion measurement. The manufacturer should supply the value of this error from the calibration study. The researcher will get the same value, apart from random sampling variation, in the validity study.
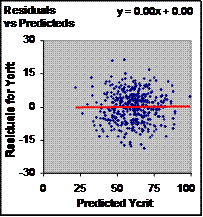
It is important to understand that the standard error of the estimate in the calibration or validity study is derived from all the subjects and therefore ought to apply to all subjects. In the second stage of the analysis, the researcher checks that the error is indeed similar for all subjects, by inspecting a plot of "residuals vs predicteds", as shown in Figure 2. The residuals are the vertical distances between the observed values and the line in Figure 1 (the standard error of the estimate is the standard deviation of the residuals). The predicteds are the corresponding Y values on the line. A plot of residuals vs predicteds provides another and better view of the scatter of points about the line. The researcher should examine the scatter for so-called heteroscedasticity (non-uniformity); for example, if there is more scatter at the high end of predicted values, the standard error of the estimate will be an underestimate of the error for such subjects, and the standard error must therefore be an overestimate for subjects with lower values. Curvature in the scatter is another kind of non-uniformity that amounts to non-linear bias; it would indicate that non-linearity had not been accounted for properly in calibration or that it had crept in since manufacture. There are procedures for investigating the extent of non-uniformity, but I will not deal with those here. Note, however, that the regression line in the residuals-predicteds plot has nothing to do with bias: it always has a slope of 0 and an intercept of 0, even when the regression line of the raw data (Figure 1) indicates that bias is present. With real data there would be no point in plotting the regression line on the residuals-predicteds plot.
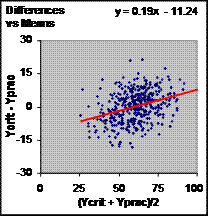
Although the residuals vs predicteds plot does not address the issue of bias, I introduced it not only because of its importance in checking for non-uniformity of error, but also because of its similarity to the Bland-Altman plot, which is shown in Figure 3. The plot can be used to check for non-uniformity of error, but more to the point of this article, a systematic trend in the values of the difference scores for different values of the mean score is supposed to indicate bias. In Figure 3 the trend line has a non-zero slope, which indicates so-called proportional bias. (In these simulations the trend line passes through the mean of the difference scores, which has an expected value of zero, so there is no so-called fixed bias.) Whether the bias is substantial is an issue I won't deal with here. The important point is that anyone checking this instrument would conclude that it had not been calibrated correctly or that the subjects in the validity study must somehow be different from those the manufacturer used to calibrate the instrument. Either conclusion would be wrong. There is nothing wrong with the instrument or the subjects. The problem is the Bland-Altman plot. A regression analysis gives the right answer: there is no bias. Of course, if bias were present, either because the instrument had been mis-calibrated or because calibration had drifted since manufacture, the regression equation for the raw values would correctly estimate its extent. The regression equation would also represent the transformation for re-calibrating the instrument to make it unbiased. Finally, the standard error of the estimate would be the random error in the re-calibrated readings, and could be compared with the manufacturer's value to check on whether the instrument had become more "noisy" since manufacture. (All of these statistics should be interpreted in conjunction with their uncertainty, represented by confidence limits, and with the smallest clinically or practically important value of the measure.) A Bland-Altman analysis provides little of this valuable information, and what it does provide can obviously be misleading. Where does the artifactual positive bias in the Bland-Altman plot come from? Or to put it another way, why is it that Ycrit-Yprac tends to be positive for the larger values of (Ycrit+Yprac)/2 and negative for the smaller values? According to Figure 1, the value produced by the instrument (Yprac) is an unbiased estimate of the criterion value (Ycrit). It follows that, for any given observed value of Yprac, Ycrit-Yprac>0 half the time and Ycrit-Yprac<0 half the time. But when Ycrit-Yprac>0, Ycrit>Yprac, so (Ycrit+Yprac)/2 will be greater than when Ycrit-Yprac<0. Therefore points on the Bland-Altman plot will have a positive slope for any given Yprac, and over the range of values of Yprac there will therefore be a positive trend. A large range for Yprac will tend to smear out the trend, which fits with the finding that the artifactual bias gets smaller as the standard error of the estimate gets smaller relative to the true between-subject standard deviation. In this article the focus has been on bias in a Bland-Altman plot of readings from an instrument when it is checked against the criterion that was used to calibrate it. The bias is an artifact of calibration of an instrument that has substantial random error. The instrument is therefore likely to show bias in a Bland-Altman plot if it is checked against other measures, criterion or otherwise. At least part of the bias will be artifactual, but the researcher will not know how much is artifact and how much is real. The Bland-Altman plot therefore should not be used to make conclusions about bias with any calibrated instrument. Those who are determined to defend the Bland-Altman approach have to find reasons to abandon regression, or more specifically least-squares regression, when calibrating the instrument. Ludbrook (2002) claimed that the presence of error in the practical variable X violated some kind of statistical assumption, but he did not explain the apparent violation or explain why least-squares regression was therefore inappropriate. My spreadsheet shows that the presence of random error in both Practical X and Criterion Y does not lead to biased prediction of Criterion Y by the Practical Y derived from the calibration. His next assertion, that "when two methods are compared, it is usual that neither can be regarded as a benchmark", is not true, in my experience: most if not all validity studies I have encountered in biomedical sciences include a measure regarded as the criterion. Researchers do not undertake validity studies without one. Ludbrook apparently wanted to put most measures on an equal footing to support his approach of least-products regression, a method of fitting a line that minimizes residuals in the vertical and horizontal direction. This approach apparently eliminates the bias problem in Bland-Altman plots, according to Atkinson and Batterham in their colloquium. But least-products regression is tantamount to giving equal weight to a practical and a criterion measure, which is unacceptable. Bias in Bland-Altman plots is not restricted to calibrated instruments: it can arise as an artifact of random error between measures that have not been calibrated. Consider two measures, Y1 and Y2, that both measure some true criterion value Y without bias, and that differ only in the amount of random error added to each. Suppose the standard deviations of the error for Y1 and Y2 are 1 and 2 units respectively, and suppose the standard deviation for Y is 5 units. The three pairwise Bland-Altman plots of these three measures all show bias! An example is included on a separate page in the spreadsheet. Evidently the Bland-Altman plot fails to correctly diagnose lack of bias even in the simple case of measures differing only in the extent of random error. On the other hand, it is easy to show with the main page of the spreadsheet that a regression analysis with Y1 as the criterion measure (Criterion Y) and Y2 as the practical measure (Practical X) does not result in bias in the prediction of either Y1 or more importantly in the prediction of the true values of Y (See Step 6a and 6b in the spreadsheet.) Bland and Altman had praiseworthy intentions when they devised new ways of dealing with measurement error. However, I think they and their followers have failed to consider that regression has more to offer than just a correlation coefficient. Previously my criticisms have focused on problems with limits of agreement, the measure of random error that Bland and Altman promoted in place of the standard error of the estimate and its equivalent in reliability studies, the standard error of measurement. (See A New View of Statistics and Hopkins, 2000.) The fact that the Bland-Altman approach is also deficient for the analysis of bias in validity studies finishes the debate as far as I am concerned. Measurement error must be analyzed with regression. I am grateful to Alan Batterham for his well-researched and generally supportive though cautious commentary. Naturally, I don't share his view that Bland-Altman plots and least-products regression might be useful in some method-comparison studies. What's needed for a comparison of two or more measures is a generic approach more powerful even than regression to model the relationship and error structure of each measure with a latent variable representing the true value. Alan and I have actually done some preliminary promising work towards this goal using mixed modeling and structural equation modeling. To view the spreadsheet within Excel rather than within the browser window, right-click on this link, select Save Target As…, save to your computer anywhere, then open. ReferencesBland JM, Altman DG (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet i, 307-310 Bland JM, Altman DG (2003). Applying the right statistics: analyses of measurement studies. Ultrasound in Obstetrics and Gynecology 22, 85-93 Hopkins WG (2000). Measures of reliability in sports medicine and science. Sports Medicine 30, 1-15 Ludbrook J (2002). Statistical techniques for comparing measurers and methods of measurement: a critical review. Clinical and Experimental Pharmacology and Physiology 29, 527–536 Published Nov 2004 |