Summarizing Data:
PRECISION
OF MEASUREMENT
continued
 MEAN
± SD or MEAN ± SEM?
MEAN
± SD or MEAN ± SEM?
The standard deviation (SD)
represents variation in the values of a variable, whereas the
standard error of the mean (SEM) represents the spread that the mean
of a sample of the values would have if you kept taking samples. So
the SEM gives you an idea of the accuracy of the mean, and the SD
gives you an idea of the variability of single observations. The two
are related: SEM = SD/(square root of sample size).
Some people think you should show SEMs with means, because they think it's
important to indicate how accurate the estimate of the mean is. And when you
compare two means, they argue that showing the SEMs gives you an idea of whether
there is a statistically significant difference
between the means. All very well, but here's why they're heading down the wrong
track:
- For descriptive statistics of your subjects, you need the SD
to give the reader an idea of the spread
between subjects. Showing an SEM with the mean is silly.
- When you compare group means, showing SDs conveys an idea of
the magnitude of the difference between the means, because you can
see how big the difference is relative to the SDs. In other words,
you can see how big the effect size
is.
- It's important to visualize the SDs when there are several
groups, because if the SDs differ too much, you may have to use
log transformation or rank
transformation before you compute confidence limits or p
values. If the number of subjects differs between groups, the SEMs
won't give you a direct visual impression of whether the SDs
differ.
- If you think it's important to indicate statistical
significance, show p values or
confidence limits of the
outcome statistic That's more accurate than showing SEMs. Besides,
does anyone know how much SEMs have to overlap or not overlap
before you can say the difference is significant? And does anyone
know that the amount of overlap or non-overlap depends on the
relative sample sizes?
- Most importantly, when you have means for pre and post
scores in a repeated-measures experiment, the
SEMs of these means do NOT give an impression of statistical significance
of the change--a subtle point that challenges many statisticians. So if the
SEMs don't show statistical significance in experiments, what's the point
of having them anywhere else?
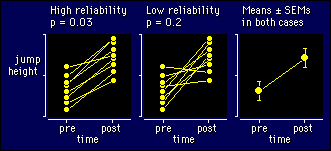
Here's a figure to illustrate why SEMs don't convey statistical
significance. It's for imaginary data in an experiment to increase
jump height. The change in height is significant (p=0.03) when the
measurement of jump height has high reliability, but not
significant (p=0.2) when the reliability is low. But the SEMs are
the same in both cases:
- The SEMs of the post-pre change scores in a treatment and control group
would indicate statistical significance. But if you show the change
scores, you should show the confidence interval for the change, not the SEM.
You should also show the SD of the change scores for the treatment and control
groups, because a substantial increase in the SD of the change scores in a
treatment group relative to a control group indicates individual
responses to the treatment. SEMs of the change scores would alert you
to the possibility of individual responses only if the sample size was the
same in both groups.
So when you see SEMs in a publication, smile, then mentally convert them into
SDs to see how big the differences are between the groups. For example, if there
are 25 subjects in a group, increase the size of the SEM by a factor of 5 (= square
root of 25) to turn it into an SD.
The bottom line: never show SEMs. Never. Trust me.
Here endeth precision of measurement and summarizing data. On the
next page we start generalizing to a
population.
Go to: Next
· Previous
· Contents ·
Search
· Home
editor
Last updated 25 June 03
