|
A New View of Statistics | |
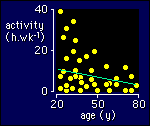 Take a look at the awful
data on the right. It's clear that activity is greater at younger ages, so you
want an outcome statistic to summarize that important finding. Fitting a line
or a curve would do the trick Let's keep it simple and fit a line, in the usual
least-squares way. The slope of the line is what you want, and its value is something
like 1.0 hours reduction in activity per decade of age. You also want confidence
limits or a p value for the slope. So how do you go about it?
Take a look at the awful
data on the right. It's clear that activity is greater at younger ages, so you
want an outcome statistic to summarize that important finding. Fitting a line
or a curve would do the trick Let's keep it simple and fit a line, in the usual
least-squares way. The slope of the line is what you want, and its value is something
like 1.0 hours reduction in activity per decade of age. You also want confidence
limits or a p value for the slope. So how do you go about it?
The least-squares approach gives you confidence limits and a p value for the slope, but you can't believe them, because the residuals are grossly non-uniform. You don't have to plot residuals vs predicteds to see that--just look how much bigger the spread is about the line for younger subjects. The bigger spread occurs for bigger values of activity, so that's a strong indication for log transformation. Unfortunately you can't take logs here, because some subjects have zero activity, and you can't take the log of zero. (You get minus infinity!) I've seen people attempt to solve this problem by adding a small number, such as 1 hour, to everyone's activity, then taking logs. I don't really agree with this approach, because it means changing some of the data.
What to do? The best approach is to use bootstrapping, but that's a big ask for most researchers. The next-best approach is to "take ranks" rather than to take logs. In other words, rank transform the dependent variable. What does that mean, exactly? Simply that you arrange the values of activity for every subject in rank order, then assign the smallest a value of 1, the next smallest a value of 2 etc., etc. Now do your modeling in the normal way, but use the variable representing the rank as the dependent variable. You have just performed a non-parametric analysis--more about that below. Rank transformation usually results in uniform residuals (same scatter for any age) for the rank-transformed variable. You should check that they are indeed uniform. If they aren't, you are no better off.
Confidence Limits via the P Value for the Rank-transformed Variable
But wait! You originally wanted confidence limits for the slope of the line of activity vs age. The analysis of rank-transformed activity will give you confidence limits for a slope, but it will be the slope of the ranks of the activity, not the slope of activity itself. The slope and its confidence limits in rank units are just about impossible to interpret, and that's true of all analyses involving rank transformation. So now what? Well, I've agonized over this one for some years, and I now have the solution. You probably won't find this one anywhere else, but I think it's the way to go.
The analysis of the rank-transformed variable gives you a p value for the outcome statistic, in this case the slope of the line. You now assume that the p value applies to the slope of the line you got by analyzing the untransformed data. Next assume you have a sample of sufficient size that the central limit theorem comes into action to give you a normal sampling distribution for your slope. Therefore combine the p value and the slope to calculate the confidence limits for the slope, using the spreadsheet for confidence limits. Done!
Confidence Limits via Cohen's Effect-size Statistic for the Rank-transformed Variable
Another approach to getting confidence limits for the outcome statistic with a rank-transformed variable is to calculate a Cohen-type effect size (change in the mean divided by a standard deviation). Again, you won't see this approach anywhere else, but again, it works well. The only drawback is that most folks still aren't used to Cohen effect sizes. Let me remind you that this outcome statistic is ideal for studies of average subjects in a population, but it's no good for studies of performance of competitive athletes.
I'll start with the simple case of the difference in the mean of two groups: for example, the mean heights of females vs males. Rank-transform height without regard to sex, then do an unpaired t test (the unequal variances version) on the rank-transformed height. Calculate the effect size for the difference between the means of two groups by taking the difference between the means of the ranked height, then dividing by the average standard deviation of the ranked variable within the two groups. (You might have to generate the average standard deviation yourself, if the t test doesn't give it to you. Average the variances, not the standard deviations, then take the square root. If you've done an ANOVA rather than a t test, the root-measn square error is the average standard deviation you want.) Divide the upper and lower confidence limits of the difference in the mean by the average standard deviation to get approximate confidence limits for the effect size.
I have checked by simulation that this Cohen-type estimate is unbiased for normally distributed variables. In other words, on average it gives the same effect size as the analysis of an untransformed normally distributed variable. Cool! Strictly speaking, the confidence limits for the effect size should be derived using something called the non-central t statistic, to take into account uncertainty in the standard deviation. With a reasonable sample size you don't have to worry about this detail. One day soon I will provide a spreadsheet to do the calculation.
You can take a similar approach to express the slope of a straight line in effect-size units, when the straight line comes from the rank-transformed variable. In this case you divide the slope and its confidence limits by the standard error of the estimate (or the root-mean square error) from the regression analysis of the rank-transformed variable. In the above example, you might get something like 0.7 Cohen units per decade, and whatever confidence limits. If you are interested in the difference over a decade, 0.7 would be a moderate effect on the scale of magnitudes. Over two decades, the difference would be 1.4 units, which would be large.
It's also possible to avoid dealing directly with the slope to express the magnitude of the effect of X on Y (here age on activity). Just rank-transform the Y, then calculate the correlation coefficient and its confidence limits. Interpret the magnitudes using the scale of magnitudes. This is the simplest and possibly the best method of all, provided you aren't particularly interested in the magnitude of the effect for different differences (sic) in X.
Your stats program will probably convert values of a variable to ranks with the click of a mouse. Or if you select non-parametric analysis in the stats program, it will do the transformation without you realizing it, because a non-parametric analysis is a parametric analysis on a rank-transformed variable. The term non-parametric refers to the fact that you are no longer modeling, for example, the means of your groups, because that information is lost when you take ranks. But you are still performing a parametric analysis, so the term is a misnomer.
The names statisticians use for non-parametric analyses are misnomers too, in my opinion: Kruskal-Wallis tests and Kolmogorov-Smirnov statistics, for example. Good grief! These analyses are simple applications of parametric modeling that belie their intimidating exotic names. But there is one name you need to know: a non-parametric correlation coefficient is called a Spearman correlation coefficient. Most stats programs will calculate this at the click of a mouse, but note that it is derived by ranking both variables. Most of the time you need to rank only the dependent variable, not the independent variable too.
Actually, some non-parametric analyses come close to being truly non-parametric--things like the signed rank-sum test. But even here you are modeling probabilities, so it's still debatable whether they should be called non-parametric. The simplest example is the sign test. It's worth a paragraph, because it tests your understanding of p values. Here's the problem: what's the minimum number of all positives or all negatives that need to come up for you to decide whether there's a significant difference? For example, if you have a group of seven athletes, and they all get better after you've done something to them, is that statistically significant? (Let's leave aside the question of a control group.) Look at it from the point of view of tossing a coin. If you toss a coin several times and get all heads or all tails, how many tosses does it take before you decide the coin is fishy? Let's start with three tosses. The chance of getting three heads or three tails is 0.5*0.5*0.5 + 0.5*0.5*0.5, i.e. 0.25, so three isn't enough. Four heads or four tails in a row occurs with a probability of 0.125, and so on until we get to six in a row (p = 0.03) and eight in a row (p = 0.008). So you need six positives or negatives in a row to declare significance at the 5% level, and eight at the 1% level.
Here's a good final question. Why not play it safe with non-uniform residuals
by doing all analyses after rank transformation? Hmmm... Well, rank transformation
throws away some information, so it can't be as good as using the original variable.
But the loss of information only starts to bite when you have small sample sizes.
In other words, with small sample sizes, non-parametric analyses are less likely
to detect effects, or the power is reduced, or the confidence intervals are
wider. So use parametric analyses wherever possible. Besides, it's easier to
interpret the outcomes from a parametric model.
Go to: Next · Previous · Contents · Search
· Home
webmaster=AT=newstats.org
Last updated 9 March 03