|
A New View of Statistics | |
![]() SAMPLE SIZE "ON THE FLY"
SAMPLE SIZE "ON THE FLY"
In the traditional approach to
research design, you use a sample big enough to detect the smallest
worthwhile effect. But hang on. You'll have wasted resources if the
effect turns out to be large, because you need a smaller sample for a
larger effect. For example, here is the confidence interval for a
correlation of 0.1 with a sample of 800, which is what you're
traditionally supposed to use to detect such correlations. Look what
happens if the correlation turns out to be 0.8:

Far too much precision for a large correlation! So wouldn't it be
better to use a smaller sample size to start with, see what you get,
then decide if you need more? You bet! I call it sample size on
the fly, because you start without knowing how many subjects you
will end up with. The official name is group-sequential
design, because you sample a group of subjects, then
another group, then another group... in sequence, until you
decide you've done enough.
I'll start this page with a potential drawback of group-sequential
designs, bias. Then I'll describe a new method based on
confidence intervals that is virtually free of bias. I'll detail the
method on separate pages for correlations,
differences between means, and
differences between frequencies. On the
last page I show how to use it for any design
and outcome, I suggest what to say when you
seek ethical
approval to use this new method,
and I give justification for a strong
warning: Do NOT
use statistical significance to reach a final sample size on the
fly. I finish that
page with a link for license holders to download a
spreadsheet that will make
calculations easier and more accurate.
![]() Big Bias Bad
Big Bias Bad
Where does this bias come from in a group sequential design? It's
easy to see. You stop if you get a big effect, but you keep going if
you get a small effect. You do the same thing again at Round #2, and
Round #3, and so on: stop on a big effect, keep going on a small
effect. Well, it's inevitable you'll end up with something higher
than it ought to be, on average. But how high? That depends on how
you start sampling and how you decide to stop. I have done
simulations to show that the bias is substantial if you use
statistical significance as your stopping rule, even for quite large
initial sample sizes (see later).
But the bias is trivial for the method I have devised using width of
confidence intervals.
![]() On the Fly with Confidence
Intervals
On the Fly with Confidence
Intervals
My method for getting sample size on the fly came out of
the conviction that confidence intervals are what make results
interesting, not statistical significance. An effect with a narrow
confidence interval tells you a lot about what is going on in a
population; an effect with a wide confidence interval tells you
little. And effects with narrow confidence intervals are publishable,
regardless of whether they are statistically significant. So all we
have to do is decide on the width of the confidence interval, then
keep sampling until we get that width. That's it, in a nutshell. The
rest is detail.
What is the appropriate width for the confidence interval? On the previous page I argued that, for very small effects, a narrow-enough 95% confidence interval is one that makes sure the population effect can't be substantially positive and substantially negative. In the case of the correlation coefficient, the width of the resulting interval is 0.20 units. It turns out that we can make this width the required width of our confidence interval for all except the highest values of correlation coefficient. Here's why.
The threshold values of correlation coefficients for the different levels of the magnitude scale are separated by 0.20 units. This separation of 0.20 units must therefore represent what we consider to be a noticeable or worthwhile difference between correlations. It follows that the confidence interval should be equal to this difference: any wider would imply an uncertainty worth worrying about; any narrower would imply more certainty than we need. It's that simple!
Acceptable widths of confidence intervals for the other effect statistics are obtained by reading them off the magnitude scale. The interval for the effect-size statistic gets wider for bigger values of the statistic. The same is true of the relative risk and odds ratio, but confidence intervals for a difference in frequencies have the same width regardless of the difference.
A bonus of having a confidence interval equal to the width of each step on the magnitude scale is that the interval can never straddle more than two steps. So when we talk about a result in qualitative terms, we can say, for example, that it is large, or moderate-large, or large-very large. But fortunately we cannot say that it is small-large or similar, which seems to be a self-contradiction.
Actually, there are occasions when you need a narrower confidence
interval. Remember that a correlation difference of 0.20 corresponds
to a change of 20% in the frequency of something in a population
group, so in matters relating to life and death an uncertainty of
less than ±10% would be desirable. Correlations in the range
0.9-1.0 also need greater precision.
Right, let's get back on the main track. How come we need smaller
samples for bigger effects? That's just the way it is with
correlations. For the same width of confidence interval, you need
less observations as the correlation gets bigger. Here's a figure
showing the necessary sample size to give our magic confidence
interval of 0.20 for various correlations:
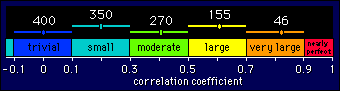
Notice that for very large correlations you need a sample size of
only 50 or so, but to nail a correlation as being small to
very small, you need more like 400. I'll
now describe the strategy for
correlations.
Go to: Next · Previous · Contents · Search
· Home
resources=AT=sportsci.org · webmaster=AT=sportsci.org · Sportsci Homepage · Copyright
©1997
Last updated 8 Dec 97