Generalizing to
a Population:
ESTIMATING SAMPLE
SIZE
continued
 SAMPLE SIZE BASED ON CONFIDENCE LIMITS
SAMPLE SIZE BASED ON CONFIDENCE LIMITS
The traditional approach
to sample size estimation requires the smallest worthwhile effects to be statistically
significant. In other words, the approach is based on the relationship between
the confidence interval and the null
value of the outcome statistic. Why such a key role for the exact null value
in the scheme of things? I believe it should be de-emphasized. If an effect is
trivial, it doesn't matter whether it is zero, slightly positive, or slightly
negative. And anyway, no real effects in nature are truly null.
So, I think it is more logical to use a sample size that ensures the true value
of the outcome could not be substantially positive and substantially negative.
In other words, the confidence interval for the outcome statistic should not
overlap into values that are substantially positive and substantial negative.
If it does overlap positive and negative values, you have to conclude
that the true value could be positive or negative. To avoid this unsatisfactory
conclusion, you need a small-enough confidence interval, which means a big-enough
sample size.
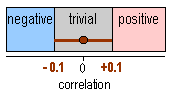 You need the biggest sample size in this new approach
when the observed value of the outcome statistic is zero or null. (You'll see
why, eventually.) The figure shows an example for an observed correlation coefficient
of zero and for ±0.10 as the smallest worthwhile effects. With a sample
size of 400, the confidence interval for an observed correlation of 0.00 is
-0.098 to +0.098, or just within ±0.10. A sample of 380 gives an exact
fit to ±0.10. Thus with 95% confidence, a population correlation coefficient
cannot be substantially positive and negative if the sample size is 380, which
is half the value you're supposed to use with the traditional approach to sample-size
estimation. The same argument and sample size apply to a descriptive study when
the outcome is the difference between the mean of two groups or the relative
frequency of something in two groups. The formulae on the previous
page are still applicable, including those for longitudinal designs (experiments
or interventions), but in all cases the sample sizes are halved. When the effects
are large, you need even smaller samples. On the next
page I show you how to get these sample sizes "on the fly".
You need the biggest sample size in this new approach
when the observed value of the outcome statistic is zero or null. (You'll see
why, eventually.) The figure shows an example for an observed correlation coefficient
of zero and for ±0.10 as the smallest worthwhile effects. With a sample
size of 400, the confidence interval for an observed correlation of 0.00 is
-0.098 to +0.098, or just within ±0.10. A sample of 380 gives an exact
fit to ±0.10. Thus with 95% confidence, a population correlation coefficient
cannot be substantially positive and negative if the sample size is 380, which
is half the value you're supposed to use with the traditional approach to sample-size
estimation. The same argument and sample size apply to a descriptive study when
the outcome is the difference between the mean of two groups or the relative
frequency of something in two groups. The formulae on the previous
page are still applicable, including those for longitudinal designs (experiments
or interventions), but in all cases the sample sizes are halved. When the effects
are large, you need even smaller samples. On the next
page I show you how to get these sample sizes "on the fly".
The fact that the sample sizes using this new approach are half those of the
old approach worries some statisticians. They say "your sample sizes give
power of 50% rather than 80% for detecting the smallest effect". That's
true, I admit, but we shouldn't be concerned with statistical significance any
more. If you accept my rationale for basing sample size on precision of estimation,
then you need half the sample size that you used to use. Or, to put it another
way, people have been using samples that are twice as big as they needed. Sure,
in one sense bigger samples are always better, because they give you more precision
for the outcome. But too much precision represents an unethical waste of resources,
so we've been getting an unethical amount of precision with our old sample sizes.
Actually, the argument is more complex, because you really need several studies
and even a meta-analysis to confirm a finding
beyond reasonable doubt. No problem.
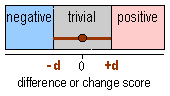 Here's
another example, this time for an experiment. The figure shows an observed outcome
of zero change and the more general case of the smallest worthwhile pre to post
difference or change of ±d. If this is a crossover or a simple experiment
without a control group, the confidence limits are ± root(2) x s/root(n) x t0.975,
df, where s is the within-subject standard deviation or typical
error, n is the sample size, and t is the value of the t statistic for cumulative
probability of 0.975 and df degrees of freedom (= n-1). Rearranging, n = 2t2s2/d2.
The value of t is approximately 2, so n is about 8s2/d2.
When n is small, t is a bit bigger than 2.0; for example, if d=s, the sample
size is about 10 rather than 8. With a control group, the sample size is 4x
as big.
Here's
another example, this time for an experiment. The figure shows an observed outcome
of zero change and the more general case of the smallest worthwhile pre to post
difference or change of ±d. If this is a crossover or a simple experiment
without a control group, the confidence limits are ± root(2) x s/root(n) x t0.975,
df, where s is the within-subject standard deviation or typical
error, n is the sample size, and t is the value of the t statistic for cumulative
probability of 0.975 and df degrees of freedom (= n-1). Rearranging, n = 2t2s2/d2.
The value of t is approximately 2, so n is about 8s2/d2.
When n is small, t is a bit bigger than 2.0; for example, if d=s, the sample
size is about 10 rather than 8. With a control group, the sample size is 4x
as big.
Go to: Next · Previous · Contents · Search
· Home
webmaster=AT=sportsci.org · Sportsci Homepage
Last updated 5 Aug 01
 You need the biggest sample size in this new approach
when the observed value of the outcome statistic is zero or null. (You'll see
why, eventually.) The figure shows an example for an observed correlation coefficient
of zero and for ±0.10 as the smallest worthwhile effects. With a sample
size of 400, the confidence interval for an observed correlation of 0.00 is
-0.098 to +0.098, or just within ±0.10. A sample of 380 gives an exact
fit to ±0.10. Thus with 95% confidence, a population correlation coefficient
cannot be substantially positive and negative if the sample size is 380, which
is half the value you're supposed to use with the traditional approach to sample-size
estimation. The same argument and sample size apply to a descriptive study when
the outcome is the difference between the mean of two groups or the relative
frequency of something in two groups. The formulae on the previous
page are still applicable, including those for longitudinal designs (experiments
or interventions), but in all cases the sample sizes are halved. When the effects
are large, you need even smaller samples. On the next
page I show you how to get these sample sizes "on the fly".
You need the biggest sample size in this new approach
when the observed value of the outcome statistic is zero or null. (You'll see
why, eventually.) The figure shows an example for an observed correlation coefficient
of zero and for ±0.10 as the smallest worthwhile effects. With a sample
size of 400, the confidence interval for an observed correlation of 0.00 is
-0.098 to +0.098, or just within ±0.10. A sample of 380 gives an exact
fit to ±0.10. Thus with 95% confidence, a population correlation coefficient
cannot be substantially positive and negative if the sample size is 380, which
is half the value you're supposed to use with the traditional approach to sample-size
estimation. The same argument and sample size apply to a descriptive study when
the outcome is the difference between the mean of two groups or the relative
frequency of something in two groups. The formulae on the previous
page are still applicable, including those for longitudinal designs (experiments
or interventions), but in all cases the sample sizes are halved. When the effects
are large, you need even smaller samples. On the next
page I show you how to get these sample sizes "on the fly".  Here's
another example, this time for an experiment. The figure shows an observed outcome
of zero change and the more general case of the smallest worthwhile pre to post
difference or change of ±d. If this is a crossover or a simple experiment
without a control group, the confidence limits are ± root(2) x s/root(n) x t0.975,
df, where s is the within-subject standard deviation or typical
error, n is the sample size, and t is the value of the t statistic for cumulative
probability of 0.975 and df degrees of freedom (= n-1). Rearranging, n = 2t2s2/d2.
The value of t is approximately 2, so n is about 8s2/d2.
When n is small, t is a bit bigger than 2.0; for example, if d=s, the sample
size is about 10 rather than 8. With a control group, the sample size is 4x
as big.
Here's
another example, this time for an experiment. The figure shows an observed outcome
of zero change and the more general case of the smallest worthwhile pre to post
difference or change of ±d. If this is a crossover or a simple experiment
without a control group, the confidence limits are ± root(2) x s/root(n) x t0.975,
df, where s is the within-subject standard deviation or typical
error, n is the sample size, and t is the value of the t statistic for cumulative
probability of 0.975 and df degrees of freedom (= n-1). Rearranging, n = 2t2s2/d2.
The value of t is approximately 2, so n is about 8s2/d2.
When n is small, t is a bit bigger than 2.0; for example, if d=s, the sample
size is about 10 rather than 8. With a control group, the sample size is 4x
as big.