WHAT IS A MODEL?
Can you see that women are usually different
from men in certain characteristics? Can you see that taller people are heavier,
in general? Can you see that participation rates differ between sports? Fine,
you're already an expert in the use of models! All we're going to do now is formalize
your intuitive understanding, and put numbers on everything. Let's hope we don't
destroy your intuition in the process!
What do these three examples have in common? Something affected by or related
to something else? Yes, a model is a relationship between variables.
The relationships we deal with are usually simple: women are shorter than men,
by a fixed amount; body mass is proportional to height or maybe height2;
the chance that any given person will participate in a particular sport is a
simple function of age, sex, socio-economic status, or whatever.
Inasmuch as models are relationships between variables, I could have dealt
with them under the general heading of Summarizing Data, and in particular in
the pages on effect statistics. Certainly, if our
only aim was to characterize the relationship in a sample, then that's where
these pages should have been. But we fit a model to data from a sample almost
always to make a statement about the model in the population. That is, we want
to make a statement about the precision of the estimate of the effect statistic(s)
describing the model, using things like confidence
limits and/or chances of clinical benefit
(or P values and/or statistical significance, if you are stuck in the 20th Century).
So I deal with models here, under the heading of Generalizing to a Population.
Let's be clear, though: a model is another way of summarizing data using effect
statistics.
On the next pages I'll get more technical about how different
kinds of variable produce different models. Meanwhile, let's take a
sneak preview of a simple model.
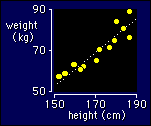Here are some
imaginary heights and weights of a sample of adults. As soon as you
plot data like these, you want to draw a straight line through them.
The straight line is the model. You decide you want to draw one, and
the stats program does the rest. It finds the equation of the
straight line that fits the data best. It also produces a
correlation coefficient, which is a measure
of how well the line fits (or, same thing, how close the relationship
between height and weight comes to being a straight line). And,
inasmuch as the data are a sample, the program even produces
confidence limits for the line, or a
p value for a test of whether there is a
line in the population at all. In fact, statistical modeling and
statistical testing mean the same thing.
Is this all too easy, or what? It gets a bit more complicated for
things like analysis of covariance, repeated measures categorical
modeling, and so on, but the principle is the same.
Go to: Next · Previous · Contents · Search
· Home
editor · Sportsci Homepage
Last updated 31 Jan 03