Generalizing to a Population: CONFIDENCE
LIMITS continued
 GETTING
IT WRONG
GETTING
IT WRONG
The words probability and confidence
seem to come up a lot. You should be getting the message that few things are definite
in our discipline, or in any empirical science. Sometimes we get it wrong.
From the point of view of confidence intervals, getting it wrong is simply
a matter of the population value being outside the confidence interval. I call
it a Type O error. You can think of the "O" as standing either
for "outside (the confidence interval)" or for "zero" (as
opposed to errors of Type I and II, which it supersedes). For 95% confidence
limits the Type O error rate is 5%, by definition. From the point of view of
hypothesis testing, getting it wrong is much more complicated. You can be responsible
for a false alarm or Type I error, and a failed alarm or
Type II error. An entirely different way to get things
wrong is to have bias in your estimate of an effect. This
page ends with a link to download a PowerPoint slide presentation,
in which I summarize and in some instances extend important points from
these pages.
 Type
I Error
Type
I Error
A level of significance of 5% is
the rate you'll declare results to be significant when there are no
relationships in the population. In other words, it's the rate of
false alarms or false positives. Such things happen, because some
samples show a relationship just by chance.
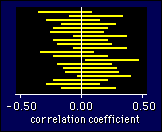 For
example, here are typical 95% confidence intervals for 20 samples of the same
size for a population in which the correlation is 0.00. (The sample size is
irrelevant.) Notice that one of the correlations is statistically significant.
If that happened to be your study, you would rush into print saying that there
is a correlation, when in reality there isn't. You would be the victim of a
Type I error. Of course, you wouldn't know until others--or you--had tested
more subjects and found a narrower confidence interval overlapping zero.
For
example, here are typical 95% confidence intervals for 20 samples of the same
size for a population in which the correlation is 0.00. (The sample size is
irrelevant.) Notice that one of the correlations is statistically significant.
If that happened to be your study, you would rush into print saying that there
is a correlation, when in reality there isn't. You would be the victim of a
Type I error. Of course, you wouldn't know until others--or you--had tested
more subjects and found a narrower confidence interval overlapping zero.
Cumulative Type
I and Type O Error Rates
The only time you need to worry about setting
the Type I error rate is when you look for a lot of effects in your data. The
more effects you look for, the more likely it is that you will turn up an effect
that seems bigger than it really is. This phenomenon is usually called the inflation
of the overall Type I error rate, or the cumulative Type I error
rate. So if you're going fishing for relationships amongst a lot of variables,
and you want your readers to believe every "catch" (significant effect), you're
supposed to reduce the Type I error rate by adjusting the p value downwards
for declaring statistical significance.
The simplest adjustment is called the Bonferroni. For
example, if you do three tests, you should reduce the p value to
0.05/3, or about 0.02. This adjustment follows quite simply from the
meaning of probability, on the assumption that the three tests are
independent. If the tests are not independent, the adjustment is too
severe.
Those of us who use confidence intervals rather than p values have to be aware
that inflation of the Type O error also happens when we report more than
one effect. For example, if there are two independent effects, the probability
that at least one will be outside its confidence interval is about 10%. We could
increase the width of our confidence intervals to bring the overall probability
back to 5%. For example, Bonferroni-adjusted 95% confidence intervals for three
effects would each be 98% confidence intervals. Adjusting the confidence intervals
in this or some other way will keep the purists happy, but I'm not sure it's
such a good idea. I prefer to see the raw 95% confidence intervals, and I prefer
to make my own mental adjustment when there are lots of effects. I just look
at the results and think to myself, OK, the population value might be outside
the interval for one or two of those effects (depending on how many results
are reported). The fact that the effects are reported in one publication is
no justification for widening the confidence intervals, in my view. You might
just as well argue that all the confidence intervals in the entire issue of
the journal should be widened, to keep the cumulative error rate for the issue
in check! And why stop with one issue... So I don't think confidence intervals
or p values should be adjusted, but I know many will disagree.
Why not use a lower p value all the time, for example a p value of
0.01, to declare significance? Surely that way only one in every 100
effects you test for is likely to be bogus? Yes, but it is harder to
get significant results, unless you use a bigger sample to narrow
down that confidence interval. In any case, you are entitled to stay
with a 5% level for one or two tests, if they are
pre-planned--in other words, if you set up the whole study
just to do these tests. It's only when you tack on a lot of other
tests afterwards (so-called post-hoc tests) that you need to
be wary of false alarms.
Controlling the Type I error comes up a lot in analysis of variance, when you
do comparisons between several groups or levels. For more insights see estimates
and contrasts in one-way ANOVA and estimates
and contrasts in repeated-measures ANOVA.
 Type
II Error
Type
II Error
The other sort of error is the
chance you'll miss the effect (i.e. declare that there is no
significant effect) when it really is there. In other words, it's the
rate of failed alarms or false negatives. Once again, the alarm will
fail sometimes purely by chance: the effect is present in the
population, but the sample you drew doesn't show it.
The smaller the sample, the more likely you are to commit a Type
II error, because the confidence interval is wider and is therefore
more likely to overlap zero. Here's an example in which a Type II
error has occurred for a correlation. Imagine you got this
result:
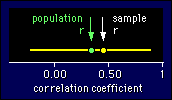 I've
indicated where the population correlation is for this example, but
of course, in reality you wouldn't know where it was. I've made the
true correlation about 0.40, which is well worth detecting. But it
hasn't been detected, because the confidence interval overlaps zero.
A big-enough sample size would have produced a confidence interval
that didn't overlap zero, in which case you would have detected a
correlation, so no Type II error would have occur red. Now, a test of
your understanding: where would the population r have to be on the
figure for a Type II error NOT to have been made? Answer: on or close
to 0.00.
I've
indicated where the population correlation is for this example, but
of course, in reality you wouldn't know where it was. I've made the
true correlation about 0.40, which is well worth detecting. But it
hasn't been detected, because the confidence interval overlaps zero.
A big-enough sample size would have produced a confidence interval
that didn't overlap zero, in which case you would have detected a
correlation, so no Type II error would have occur red. Now, a test of
your understanding: where would the population r have to be on the
figure for a Type II error NOT to have been made? Answer: on or close
to 0.00.
The Type II error needs to be considered explicitly at the time
you design your study. That's when you're supposed to work out the
sample size needed to make sure your
study has the power to detect anything useful. For this
purpose the usual Type II error rate is set to 20%, or 10% for really
classy studies. The power of the study is sometimes referred to as
80% (or 90% for a Type II error rate of 10%). In other words, the
study has enough power to detect the smallest worthwhile effects 80%
(or 90%) of the time.
Here's something interesting that no-one seems to mention: cumulative Type
II error rate--in other words, the chance that you will miss at least one
effect when you test for more than one. Is your head starting to spin? Mine
is! Don't worry, just go back to confidence limits and the notion of cumulative
Type O error. When you are looking at lots of effects, the near equivalent of
inflated Type II error is the increased chance that any one of the effects will
be bigger than you think it could be (bigger than its upper confidence limit).
Come to think of it, the near equivalent of inflated Type I error is the increased
chance that any one of the effects will be smaller than you think.
 Bias
Bias
People use the term bias to
describe deviation from the truth. That's the way we use the term in
statistics, too: we say that a statistic is biased if the average
value of the statistic from many samples is different from the value
in the population. To put it simply, the value from a sample tends to
be wrong.
The easiest way to get bias is to use a sample that is in some way a non-random
sample of the population: if the average subject in the sample tends to be different
from the average person in the population, the effect you are looking at could
well be different in the sample compared with the population.
Some statistics are biased, if we calculate them in the wrong way. Using n
instead of n-1 to work out a standard deviation is
a good example. There is also bias in some reliability
statistics. Building up a sample size in stages can also result in bias,
as I describe in sample size on the fly.
 SLIDES
ON CONFIDENCE LIMITS
SLIDES
ON CONFIDENCE LIMITS
Click here
to download a PowerPoint 97/98 set of 30 slides on the topic
"Planning, Performing, and Publishing Research with Confidence
Limits", which I presented on this topic at the annual meeting of the
American College of Sports Medicine in Seattle, June 4 1999. If you
have trouble downloading or opening the file, click
here.
Go to: Next
· Previous
· Contents ·
Search
· Home
webmaster=AT=newstats.org
Last updated 18 June 00
 For
example, here are typical 95% confidence intervals for 20 samples of the same
size for a population in which the correlation is 0.00. (The sample size is
irrelevant.) Notice that one of the correlations is statistically significant.
If that happened to be your study, you would rush into print saying that there
is a correlation, when in reality there isn't. You would be the victim of a
Type I error. Of course, you wouldn't know until others--or you--had tested
more subjects and found a narrower confidence interval overlapping zero.
For
example, here are typical 95% confidence intervals for 20 samples of the same
size for a population in which the correlation is 0.00. (The sample size is
irrelevant.) Notice that one of the correlations is statistically significant.
If that happened to be your study, you would rush into print saying that there
is a correlation, when in reality there isn't. You would be the victim of a
Type I error. Of course, you wouldn't know until others--or you--had tested
more subjects and found a narrower confidence interval overlapping zero. I've
indicated where the population correlation is for this example, but
of course, in reality you wouldn't know where it was. I've made the
true correlation about 0.40, which is well worth detecting. But it
hasn't been detected, because the confidence interval overlaps zero.
A big-enough sample size would have produced a confidence interval
that didn't overlap zero, in which case you would have detected a
correlation, so no Type II error would have occur red. Now, a test of
your understanding: where would the population r have to be on the
figure for a Type II error NOT to have been made? Answer: on or close
to 0.00.
I've
indicated where the population correlation is for this example, but
of course, in reality you wouldn't know where it was. I've made the
true correlation about 0.40, which is well worth detecting. But it
hasn't been detected, because the confidence interval overlaps zero.
A big-enough sample size would have produced a confidence interval
that didn't overlap zero, in which case you would have detected a
correlation, so no Type II error would have occur red. Now, a test of
your understanding: where would the population r have to be on the
figure for a Type II error NOT to have been made? Answer: on or close
to 0.00.