Generalizing to a
Population:
REPEATED-MEASURES
MODELS continued
 Other
Repeated-Measures Models
Other
Repeated-Measures Models
I deal with several here: an extra
between-subject effect (example: male and female subjects), two
or more within-subject factors (example: the same subjects get several treatments
at several time points), a general type of within-subject model
(you fit data to each subject separately, then combine the fits), inclusion of
covariates in the model to analyze for individual responses,
trends in repeated sets of trials, and mechanisms, and finally troublesome
variables that might require transformation or more advanced approaches.
An Extra Between-Subject
Effect
model: numeric <= (subject) trial group trial*group
sex sex*trial sex*group sex*trial*group
or simply: numeric <= (subject) trial | group | sex
example: jumphgt <= (athlete) time | group
| sex
I've used the first example from the previous page. The
only difference is that we now know our subjects are a mixture of males and
females. The analysis gets complicated, because sex could affect everything--that's
why there are so many interaction terms in the model. But we're usually interested
only in the extent to which the sexes differ for the effect of the treatment,
so that means comparing the appropriate levels of sex*trial*group. In short,
find the levels for trial*group that tell you what you want to know, then find
the difference between those for the females and those for the males in the
sex*trial*group term.
A word of warning! The term trial*group gives you the overall
effect of the treatment between the experimental and control groups,
but with sex in the model it's the average of the effect on the
females and males. In other words, it's the expected effect of the
treatment with equal numbers of males and females, even though your
sample may have had unequal numbers.
The simple notation of a vertical bar ( | ) between effects is
what the Statistical Analysis System uses to indicate that you want
to include all possible main effects and interactions in the
analysis. I usually leave them all in, because I subscribe to the
idea that all independent variables have some effect on the outcome
variable, however small. The only harm that can come from including
all the interaction terms is loss of degrees of freedom, and
therefore widening of the confidence intervals. On the other hand, if
the effects of sex on the treatment are substantial, then inclusion
of sex*trial*group will actually make the confidence intervals
smaller, because it will eliminate the variability in the effect of
the treatment that was due to sex.
In any case, if the effect of sex is substantial, you will want to
know about it! For that reason, if the outcome of your study is as
important for males as for females, you should try to have equal
numbers of male and female subjects. Your confidence interval for the
overall effect on females and males combined will be only a bit wider
than if you had subjects of one sex, but of course the effect will be
the average of the effect on (equal numbers of) females and males.
The sex*trial*group interaction will tell you how different the males
are from the females, although the confidence interval for the
comparison of the effect on females and males will be about twice as
wide as that for the overall effect. So, to properly delimit the
difference between females and males, you will need four times as
many subjects as for a single-sex study. That's the bad news. The
good news is that you will end up with a wonderfully narrow
confidence interval for the overall effect.
Two or More
Within-Subject Effects
model: numeric <= (subject) trial condition trial*condition
example: jumphgt <= (athlete) time test time*test
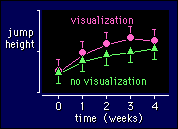 Imagine
that the intervention is a program aimed at training athletes to use visualization
before a jump (and thereby jump higher). At weekly intervals the athletes perform
a jump with and without visualization. The figure shows a possible outcome,
in which visualization starts to work after a couple of weeks of training:
Imagine
that the intervention is a program aimed at training athletes to use visualization
before a jump (and thereby jump higher). At weekly intervals the athletes perform
a jump with and without visualization. The figure shows a possible outcome,
in which visualization starts to work after a couple of weeks of training:
The model has the same form as in the previous example, but I've
replaced group (representing separate measurements on different
subjects) with condition (representing separate measurements on the
same subjects). The interpretation of trial and condition in the
model is the same as that for trial and group. Coaxing your stats
program to deal with two or more within-subject effects will be a
challenge!
In the example, I've renamed trial and condition to time and test
to make things a bit clearer. The interpretation of time is obvious.
Test represents the test of jump height, and it has two levels:
visualization and no visualization. The interaction effect time*test
tells us about the difference between the two time courses, and
contrasts between the different levels of time and test for this
effect tell us when the effect of visualization differs from no
visualization. A polynomial contrast would show a substantial
difference in linear and quadratic components, indicating that
jumping with visualization shows a more rapid improvement in jump
height initially (the linear effect), but that the gap is closing by
Week 4 (the quadratic effect). You'll have to think really hard about
this one.
An unsophisticated approach to these data would be to perform a series of paired
t tests for each time point. For example, you might find that the difference
between visualization and no visualization is significant at Weeks 2 and 3,
but not at the other times. This approach does not take into account any difference
between the tests at Week 0, so it's not valid. An acceptable fix is to subtract
the jump height at Week 0 from that at each of the other weeks (for the two
tests separately), then do a paired t test to compare visualization with no
visualization at Weeks 1 through 4.
Within-Subject Modeling
This is a name I've devised for an approach
that reduces or avoids the complexity of repeated-measures analyses. Basically,
you derive a single measurement from the repeated measurements on each subject,
then apply an appropriate simple analysis to the single measurement. The post-pre
change score is the simplest example of a single measurement, and you would
analyze the change scores with the unequal-variances version of the unpaired
t statistic.
The approach works well for more complex derived measurements, too. For example,
imagine you're looking at the effect of overtraining on recovery of heart rate
following a standard bout of exercise. Let's say you record heart rate at half-minute
intervals for three minutes. OK, that makes seven repeated measurements. Do
you use repeated-measures ANOVA on these heart rates? Well, you could, I suppose.
But what about if you want to fit an exponential decay curve on the heart rates,
and extract the time constant. I defy anyone to deal with that within a repeated-measures
model. It's only possible if you fit an exponential curve to each subject's
data separately, extract a time constant for each subject, then use the time
constant in your subsequent analyses. Hence the name within-subject modeling:
you fit the same model to each subject and extract one or more parameters, which
you then use for further analysis. r.
In fitting the model to each subject, you don't have to worry about distributions
of residuals. Subsequent modeling with the parameters does need to be done properly,
though. That modeling could be cross-sectional or longitudinal (repeated measures).
For example, if the seven measurements of heart rate are taken on only one occasion
for each subject, subsequent analysis of the parameter(s) describing the change
in heart rate will be cross-sectional. But if the seven measurements are taken
on several occasions, each subject provides several estimates of the parameter(s),
so repeated-measures modeling will be necessary.
A real advantage of within-subject modeling is that most research students
can do it without complex statistical analyses. Another advantage is that the
analyses require fewer assumptions about the repeated-measures structure of
the data, so the p values and confidence limits are more trustworthy. But mixed
modeling, properly applied, is more powerful, especially when you want to include
covariates in the analysis. See the slideshow on repeated measures for more
examples and explanations of within-subject modeling.
Covariates in
Repeated-Measures Analyses
By adding terms called covariates
to the usual (fixed-effects) model, you can analyze for the following: the extent
to which a subject characteristic accounts for individual responses to
a treatment, the effect of the treatment on trends in repeated sets of trials,
and the extent to which the effect of the treatment was due to changes in a
putative mechanism variable. All is explained in the slideshow on repeated
measures that I referred to on the first page on
repeated measures. Click
here to download the slideshow, which is an updated and extended version
of an earlier slideshow
on covariates in repeated measures.
Repeated-Measures
Analysis of Troublesome Variables
In earlier pages on non-repeated-measures
models, I showed how to deal with dependent variables that don't produce uniform
normally distributed residuals. The same approaches apply to repeated-measures
models. Thus, you will often need to log-transform
or rank-transform a variable before analyzing it.
When you rank-transform, make sure you do it to all the observations in one
shot, not to each repeated measurement separately. The data will need to be
in the form of one row per trial (as for mixed modeling), not one row per subject
(as for ANOVA), for you to do the rank transformation correctly within an Excel
spreadsheet.
An exact analysis of ordinal variables, such as those derived from Likert scales,
requires repeated-measures logistic regression, but the analyses are difficult
for newbies and the outcome statistics (odds ratios) are hard to interpret.
For most variables, including even those with only two levels (yes or no, injured
or not...), you can code each level of the variable as consecutive integers
(0 and 1; 1, 2, 3, 4, and 5; and so on) and analyze it as if it was a well-behaved
continuous normally distributed variable. Sure, the residuals are anything but
normal, but as before, you can count on the central
limit theorem to make the sampling distribution of the effect statistic
normal, so the confidence limits or p values will be trustworthy. If responses
for one or more groups are severely stacked up at one end of the scale, you
will need a large sample size (possibly >20) for the central limit theorem
to do its thing. I can't say exactly how many, but I hope to do some simulations
to get an idea. The unequal-variances t test came through with flying colors
for modest sample sizes (10-20) in my simulations with non-repeated-measures
ordinal variables, and it will probably do equally well when applied to change
scores derived from ordinal variables. We can't assume that mixed modeling will
perform as well, because its method of estimation is different from that in
the t test. Simulation will reveal all.
Nominal dependent variables can be analyzed by repeated-measures categorical
modeling, if you want outcomes expressed as odds ratios. Otherwise treat each
level of the nominal variable as a separate variable coded 0 or 1 (as I suggested
under categorical modeling), then analyze each variable
with conventional repeated-measures approaches. For example, you get schoolkids
to tick one of four boxes representing the most important reason for playing
sport. You collect the questionnaire, then show half of them a video aimed at
convincing them that winning is (or isn't) everything. Finally you give them
a fresh copy of the questionnaire to fill in. To what extent did the video change
their attitude? You might even administer the questionnaire again a month later
to see how the changes lasted. To do the analysis, treat each reason as a separate
variable, code it 1 if the kid ticked it, or 0 if not, then use the unequal-variances
t statistic to investigate differences in the changes between the group who
saw the video and those who didn't. The magnitude of the outcome is the proportion
of kids who changed their choice of the given reason.
Variables representing proportions or counts require root or arcsine-root transformation
before you give them the usual repeated-measures analysis. The more exact approach
is to use binomial or Poisson regression. Proc Genmod in SAS does it for repeated
measures.
The next page deals specifically with the use
of mixed modeling in the Statistical Analysis System.
Go to: Next
· Previous
· Contents ·
Search
· Home
webmaster
Last updated 8 June 03
 Imagine
that the intervention is a program aimed at training athletes to use visualization
before a jump (and thereby jump higher). At weekly intervals the athletes perform
a jump with and without visualization. The figure shows a possible outcome,
in which visualization starts to work after a couple of weeks of training:
Imagine
that the intervention is a program aimed at training athletes to use visualization
before a jump (and thereby jump higher). At weekly intervals the athletes perform
a jump with and without visualization. The figure shows a possible outcome,
in which visualization starts to work after a couple of weeks of training: