model: numeric <= nominal1 nominal2 nominal1*nominal2
example: training <= sex sport sex*sport
|
A New View of Statistics |
|
![]() Two-Way
ANOVA
Two-Way
ANOVA
model:
numeric <= nominal1 nominal2 nominal1*nominal2
example: training <= sex sport
sex*sport
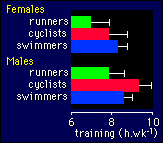 This
model is like a one-way ANOVA with an extra grouping variable. I've
put the groups up the Y axis to make it easier to show the names of
the sports. The outcome variable (hours of training per week) is
still the dependent variable, even though it is shown on the X axis.
By the way, the two in two-way ANOVA refers to the two
main effects in the model, not to the two levels for sex in this
example. So a three-way ANOVA would have three main effects, and so
on. Now let's see what each effect in the model tells us about the
effects of sex and sport on training.
This
model is like a one-way ANOVA with an extra grouping variable. I've
put the groups up the Y axis to make it easier to show the names of
the sports. The outcome variable (hours of training per week) is
still the dependent variable, even though it is shown on the X axis.
By the way, the two in two-way ANOVA refers to the two
main effects in the model, not to the two levels for sex in this
example. So a three-way ANOVA would have three main effects, and so
on. Now let's see what each effect in the model tells us about the
effects of sex and sport on training.
The main effects are easy to understand. Sex tells us how different the training is between sexes overall. In these data it's obvious that the males are doing more training than the females. The numeric value for the difference would be given by the values of the two levels for sex in the solution for the model. You would get your program to perform an estimate or a contrast between the two levels of sex to get confidence intervals or p values. Note that the resulting value for the difference between sexes is equivalent to the difference you would get between the means for the males and the females with equal numbers of males and females in each of the three sports. If you have different numbers in each sport, the difference between the raw means for all the males and all the females will be different from the stats program's estimate of the difference. The estimate from the stats program is usually the one you're interested in.
In a similar fashion, the sport effect gives overall differences between the sports. You would do pairwise estimates or contrasts to see how different the sports are from each other. In the example, runners are clearly different from cyclists and swimmers, but cyclists are about the same as swimmers, because the difference goes one way for females and the other way for males. Again, the estimates for the differences between sports are the same as what you would get with equal numbers of males and females in each sport.
Which leaves us with the interaction. It tells us about the overall trend for differences in the sports within females compared with the trend within males. Well, it looks like something interesting is going on with the trends, because the means for the cyclists and swimmers swap over between females and males. To find out how big the differences are, you would do estimates or contrasts for the different levels of the interaction term. There are six levels in sex*sport: two for sex, and three for sport. In alphabetical order, the levels are female·cyclists, female·runners, female·swimmers, male·cyclists, male·runners, male·swimmers. The estimate of the magnitude of the female-male swap over for the cyclists and swimmers would be given by the value for (male·cyclists - male·swimmers) - (female·cyclists - female·swimmers). This difference in the differences is about one hour, so you'd say "males did relatively more cycling than swimming in comparison with females; the combined difference was about an hour..." And as before, think about the difference as what you would get with equal numbers of males and females in each sport.
With luck your stats program will calculate confidence limits for all the differences between groups. It will certainly calculate p values anyway, and you can convert these to confidence limits by downloading a spreadsheet.
Don't forget to keep one eye on the standard deviations when you
compare means of groups. In the above example, many of the
differences between groups are equivalent to at least one standard
deviation (an effect size of at least 1.0), so they are moderate to
large. Differences between standard deviations are also important.
Notice that the standard deviations for the swimmers are about half
those in the other sports. Maybe the swimmers all train in squads
with similar training programs. That could be a problem, in more ways
than one. First, if the subjects are drawn from just a few
squads, their values of training will not be independent of each
other, so we'll have to use repeated-measures modeling. And secondly,
different standard deviations violate an assumption our usual
analyses are based on. We can get around this problem by transforming
the training times. Log transform? No,
the standard deviations would need to be bigger for more training.
Rank transform? Yes, non-parametric
analysis is called for here. Just rank the entire column of data for
training, then do the analysis as usual.
Go to: Next
· Previous
· Contents ·
Search
· Home
resources=AT=sportsci.org
·
webmaster=AT=sportsci.org
·
Sportsci
Homepage
·
Copyright
©1999
Last updated 17 June 99